
【题目】【2016高考江苏卷】已知函数![]() .设
.设![]() .
.
(1)求方程![]() 的根;
的根;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若![]() ,函数
,函数![]() 有且只有1个零点,求
有且只有1个零点,求![]() 的值。
的值。
【答案】(1)①0 ②4(2)1
【解析】
试题分析:(1)①根据指数间倒数关系![]() 转化为一元二次方程
转化为一元二次方程![]() ,求方程根②根据指数间平方关系
,求方程根②根据指数间平方关系![]() ,将不等式转化为一元不等式,再利用变量分离转化为对应函数最值,即
,将不等式转化为一元不等式,再利用变量分离转化为对应函数最值,即![]() 的最小值,最后根据基本不等式求最值(2)先分析导函数零点情况:唯一零点
的最小值,最后根据基本不等式求最值(2)先分析导函数零点情况:唯一零点![]() ,再确定原函数单调变化趋势:先减后增,从而结合图像确定唯一零点必在极值点
,再确定原函数单调变化趋势:先减后增,从而结合图像确定唯一零点必在极值点![]() 取得,而
取得,而![]() ,因此极值点
,因此极值点![]() 必等于零,进而求出
必等于零,进而求出![]() 的值.本题难点在证明
的值.本题难点在证明![]() ,这可利用反证法:若
,这可利用反证法:若![]() ,则可寻找出一个区间
,则可寻找出一个区间![]() ,由
,由![]() 结合零点存在定理可得函数存在另一零点,与题意矛盾,其中可取
结合零点存在定理可得函数存在另一零点,与题意矛盾,其中可取![]() ;若
;若![]() ,同理可得.
,同理可得.
试题解析:(1)因为![]() ,所以
,所以![]() .
.
①方程![]() ,即
,即![]() ,亦即
,亦即![]() ,
,
所以![]() ,于是
,于是![]() ,解得
,解得![]() .
.
②由条件知![]() .
.
因为![]() 对于
对于![]() 恒成立,且
恒成立,且![]() ,
,
所以![]() 对于
对于![]() 恒成立.
恒成立.
而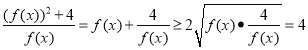 ,且
,且![]() ,
,
所以![]() ,故实数
,故实数![]() 的最大值为4.
的最大值为4.
(2)因为函数![]() 只有1个零点,而
只有1个零点,而![]() ,
,
所以0是函数![]() 的唯一零点.
的唯一零点.
因为![]() ,又由
,又由![]() 知
知![]() ,
,
所以![]() 有唯一解
有唯一解![]() .
.
令![]() ,则
,则![]() ,
,
从而对任意![]() ,
,![]() ,所以
,所以![]() 是
是![]() 上的单调增函数,
上的单调增函数,
于是当![]() ,
,![]() ;当
;当![]() 时,
时,![]() .
.
因而函数![]() 在
在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数.
上是单调增函数.
下证![]() .
.
若![]() ,则
,则![]() ,于是
,于是![]() ,
,
又![]() ,且函数
,且函数![]() 在以
在以![]() 和
和![]() 为端点的闭区间上的图象不间断,所以在
为端点的闭区间上的图象不间断,所以在![]() 和
和![]() 之间存在
之间存在![]() 的零点,记为
的零点,记为![]() . 因为
. 因为![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 与“0是函数
与“0是函数![]() 的唯一零点”矛盾.
的唯一零点”矛盾.
若![]() ,同理可得,在
,同理可得,在![]() 和
和![]() 之间存在
之间存在![]() 的非0的零点,矛盾.
的非0的零点,矛盾.
因此,![]() .
.
于是![]() ,故
,故![]() ,所以
,所以![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=3,AD=4.现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
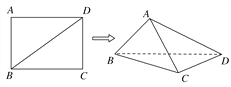
(1)试问:在折叠的过程中,直线AB与CD能否垂直?若能,求出相应a的值;若不能,请说明理由;
(2)求四面体A-BCD体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() .点
.点![]() 是椭圆
是椭圆![]() 在
在![]() 轴上方的动点,且△
轴上方的动点,且△![]() 的周长为16.
的周长为16.
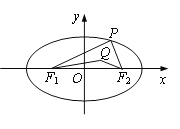
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 到△
到△![]() 三边的距离均相等.
三边的距离均相等.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②求证:点![]() 在定椭圆上.
在定椭圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
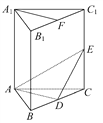
【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届河北省衡水中学高三上学期六调】已知函数![]() ,其中
,其中![]() 均为实数,
均为实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,若对任意的
,若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4 μg时治疗疾病有效,假若某病人一天中第一次服药为上午7:00,问:一天中怎样安排服药时间(共4次)效果最佳?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲![]() 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为![]() 万元,且
万元,且![]() (
(![]() ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为![]() (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;
(2)为了让年利润![]() 不低于2360万元,求年产量
不低于2360万元,求年产量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com