
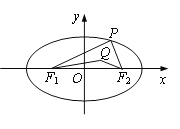
【题目】在平面直角坐标系xOy中,已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() .点
.点![]() 是椭圆
是椭圆![]() 在
在![]() 轴上方的动点,且△
轴上方的动点,且△![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 到△
到△![]() 三边的距离均相等.
三边的距离均相等.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②求证:点![]() 在定椭圆上.
在定椭圆上.
【答案】(1) ![]() ;(2)①
;(2)①![]() ;②证明见解析.
;②证明见解析.
【解析】试题分析:(1)由题意可得![]() 的值,再由隐含条件求得
的值,再由隐含条件求得![]() ,则椭圆方程可求;(2)①求出
,则椭圆方程可求;(2)①求出![]() 点坐标,设出
点坐标,设出![]() 的坐标,结合点
的坐标,结合点![]() 到
到![]() 三边的距离均相等列方程组求得点
三边的距离均相等列方程组求得点![]() 的坐标;②根据三角形面积以及椭圆的定义列方程组,可得
的坐标;②根据三角形面积以及椭圆的定义列方程组,可得![]() ,
, ![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() , 所以点
, 所以点![]() 在定椭圆上.
在定椭圆上.
试题解析:(1)依题意, ![]() ,
, ![]() ,所以
,所以![]() ,从而
,从而![]() , 故椭圆方程为
, 故椭圆方程为![]() ,(2)①当
,(2)①当![]() 时,
时, ![]() , 则直线
, 则直线![]() 的方程为:
的方程为: ![]() ,直线
,直线![]() 的方程为:
的方程为: ![]() ,
,
所以![]() ,且
,且![]() ,其中
,其中![]() ,解得
,解得![]() ,
, ![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() ;
;
②设![]() ,则点
,则点![]() 到△
到△![]() 三边的距离均为
三边的距离均为![]() ,由
,由![]() ,
,
得![]() ,其中
,其中![]() ,所以
,所以![]() ,则直线
,则直线![]() 的方程为:
的方程为: ![]() ,即
,即![]() , 所以
, 所以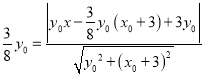 ,且
,且![]() , 且
, 且![]() , 化简得,
, 化简得, 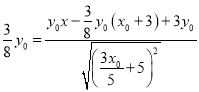 ,解得
,解得![]() ,
,
将![]() ,
, ![]() 代入
代入![]() ,得
,得![]() , 所以点
, 所以点![]() 在定椭圆上.
在定椭圆上.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数),每人每年可创利b万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的![]() ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥P-ABCD中,底面边长为2,侧棱长为![]() ,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.
,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.
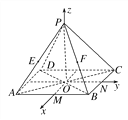
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]()
的中点,AC⊥平面BCC1B1.
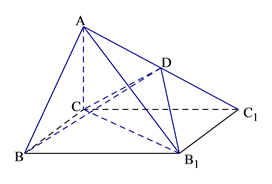
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求三棱锥C-DB1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考江苏卷】已知函数![]() .设
.设![]() .
.
(1)求方程![]() 的根;
的根;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若![]() ,函数
,函数![]() 有且只有1个零点,求
有且只有1个零点,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在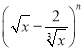 的展开式中,第5项的系数与第3项的系数之比是56:3.
的展开式中,第5项的系数与第3项的系数之比是56:3.
(1)求展开式中的所有有理项;
(2)求展开式中系数绝对值最大的项.
(3)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com