
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,
上一点, ![]() 平面
平面![]() .
.
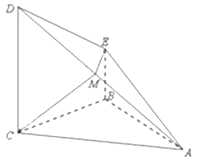
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)详见解析,(Ⅱ)2.
【解析】试题分析:(1)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,得出
,得出![]() ,再由
,再由![]() 平面
平面![]() ,证得
,证得![]() 平面
平面![]() ,进而利用线面平行的判定定理,即可证得
,进而利用线面平行的判定定理,即可证得![]() 平面
平面![]() ;
;
(2) 连接![]() ,得出
,得出![]() ,由(1)得出
,由(1)得出![]() ,因为
,因为![]() 是
是![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中点,进而得出
的中点,进而得出![]() 平面
平面![]() ,利用棱锥的体积公式,即可求解几何体的体积。
,利用棱锥的体积公式,即可求解几何体的体积。
试题解析:
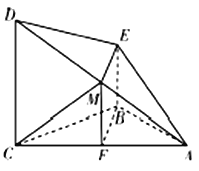
(Ⅰ)证明:取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:连接![]() ,因为
,因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
由(Ⅰ)知![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数(![]() ,简称
,简称![]() )是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为
)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为![]() 等六项.空气质量按照
等六项.空气质量按照![]() 大小分为六级:一级
大小分为六级:一级![]() 为优;二级
为优;二级![]() 为良好;三级
为良好;三级![]() 为轻度污染;四级
为轻度污染;四级![]() 为中度污染;五级
为中度污染;五级![]() 为重度污染;六级
为重度污染;六级![]() 为严重污染.
为严重污染.
某人根据环境监测总站公布的数据记录了某地某月连续10天![]() 的茎叶图如图所示:
的茎叶图如图所示:

(1)利用访样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算);
)的天数;(按这个月总共30天计算);
(2)若从样本中的空气质量不佳(![]() )的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
)的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=3,AD=4.现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
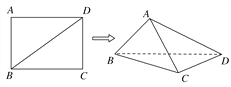
(1)试问:在折叠的过程中,直线AB与CD能否垂直?若能,求出相应a的值;若不能,请说明理由;
(2)求四面体A-BCD体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.

求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2,3,4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球(左右手依次各取两球为两次取球)的成功取法次数为随机变量X,求X的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
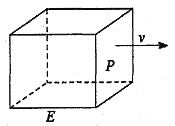
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:
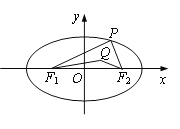
【题目】在平面直角坐标系xOy中,已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() .点
.点![]() 是椭圆
是椭圆![]() 在
在![]() 轴上方的动点,且△
轴上方的动点,且△![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 到△
到△![]() 三边的距离均相等.
三边的距离均相等.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②求证:点![]() 在定椭圆上.
在定椭圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4 μg时治疗疾病有效,假若某病人一天中第一次服药为上午7:00,问:一天中怎样安排服药时间(共4次)效果最佳?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com