练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题共12分）
    已知函数f(x)＝2x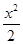－－aln(x＋1)，a∈R．（1）若a＝－4，求函数f(x)的单调区间；
    （2）求y＝f(x)的极值点（即函数取到极值时点的横坐标）．

    （1）f(x)的单调增区间为（-1,3）， 单调减区间为（3,+∞）。
    （2）
    ⅰ.7分
    ⅱ.当时，若,由函数的单调性可知f(x)有极小值点；有极大值点。若时，f(x)有极大值点,无极小值点。

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    (本小题13分)已知函数
    （1）在右图给定的直角坐标系内画出的图象；
    （2）写出的单调递增区间．
    (3) 求的最小值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某公司生产一种产品的固定成本是10000元，每生产一件产品需要另外投入80元，又知市场对这种产品的年需求量为800件，且销售收入函数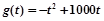，其中t是产品售出的数量，且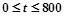（利润=销售收入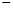成本）.
    （1）若x为年产量，y表示利润，求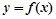的解析式；
    （2）当年产量为多少时，求工厂年利润的最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）
    某工厂去年的某产品的年销售量为100万只，每只产品的销售价为10元，每只产品固定成本为8元．今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计销售量从今年开始每年比上一年增加10万只，第n次投入后，每只产品的固定成本为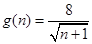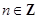（且n≥0），若产品销售价保持不变，第n次投入后的年利润为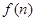万元．
    （Ⅰ）求出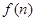的表达式；
    （Ⅱ）若今年是第1年，问第几年年利润最高?最高利润为多少万元?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)=x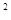+2ax+2,   x.
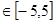    (1)当a=-1时，求函数的最大值和最小值；
    (2) 若y=f(x)在区间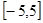 上是单调 函数，求实数  a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出场单价就降低0.02元，根据市场调查，销售商一次订购量不会超过600件．
    (1)设一次订购x件，服装的实际出厂单价为p元，写出函数p＝f(x)的表达式；
    (2)当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了保护水资源，提倡节约用水，某市对居民生活用水收费标准如下：每户每月用水不超过6吨时每吨3元，当用水超过6吨但不超过15吨时，超过部分每吨5元，当用水超过15吨时，超过部分每吨10元。
    （1）求水费y（元）关于用水量x（吨）之间的函数关系式；
    （2）若某户居民某月所交水费为93元，试求此用户该月的用水量。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分14分）某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数： ，其中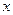是仪器的月产量。
    （1）将利润表示为月产量的函数；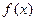
    （2）当月产量为何值时，公司所获利润最大？最大利润为多少元？
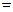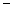    （利润总收益总成本）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）有甲、乙两种商品，经营销售这两种商品所能获得的利润依次是P和Q(万元)，它们与投入资金x(万元)的关系有经验公式:P=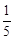x，Q=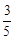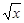.今有3万元资金投入经营甲、乙两种商品，为获得最大利润，对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少？

    查看答案和解析>>

    同步练习册答案