
(本小题13分)已知函数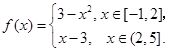
(1)在右图给定的直角坐标系内画出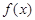 的图象;
的图象;
(2)写出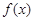 的单调递增区间.
的单调递增区间.
(3) 求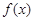 的最小值。
的最小值。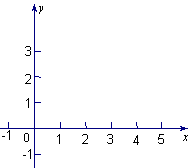
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
(14分)病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量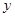 (毫克)与时间
(毫克)与时间 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数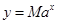 (
(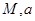 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数 的解析式;
的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?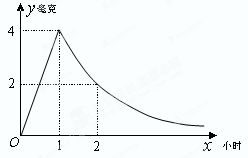
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知y= 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求 的解析式;
的解析式;
(2)求函数 的单调递减区间及值域..
的单调递减区间及值域..
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知f(x)=logax,g(x)=2loga(2x+t-2)(a>0,a≠1,t∈R).
(1)当t=4,x∈[1,2],且F(x)=g(x)-f(x)有最小值2时,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数f(x)=2x-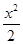 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com