
分析 (1)根据m的范围,求出集合B即可;
(2)通过讨论m的范围得到关于m的不等式组,解出即可.
解答 解∵不等式x2-x+(m-m2)<0⇒(x-m)•[x-(1-m)]<0…(2分)
(1)当$m<\frac{1}{2}$时,m<1-m,∴集合B={x|m<x<1-m}. …(4分)
(2)依题意得B?A,…(5分)
∵A={x|-1≤x≤2},
①当m<$\frac{1}{2}$时,B={x|m<x<1-m},
此时$\left\{{\begin{array}{l}{m≥-1}\\{1-m≤2}\end{array}}\right.⇒-1≤m<\frac{1}{2}$;…(7分)
②当m=$\frac{1}{2}$时,B=∅,有B?A成立;…(9分)
③当m>$\frac{1}{2}$时,B={x|1-m<x<m},
此时$\left\{{\begin{array}{l}{m≤2}\\{1-m≥-1}\end{array}}\right.⇒\frac{1}{2}<m≤2$;…(11分)
综上所述,m的取值范围是-1≤m≤2…(12分)
点评 本题考查了集合的包含关系,考查分类讨论思想以及充分必要条件,是一道中档题.


科目:高中数学 来源: 题型:解答题
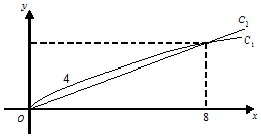 销售甲、乙两种商品所得利润分别是y1,y2万元,它们与投入资金x万元的关系分别为y1=m$\sqrt{x+1}$+a,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示.
销售甲、乙两种商品所得利润分别是y1,y2万元,它们与投入资金x万元的关系分别为y1=m$\sqrt{x+1}$+a,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知在四边形ABCD中,AD⊥CD,AD=5,AB=7,BD=8,∠BCD=135°.
如图所示,已知在四边形ABCD中,AD⊥CD,AD=5,AB=7,BD=8,∠BCD=135°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-1,1) | C. | (-1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com