
| A. | $\frac{{\sqrt{13}+1}}{3}$ | B. | $\frac{{\sqrt{7}+\sqrt{3}}}{3}$ | C. | $\sqrt{7}$+$\sqrt{3}$ | D. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ |
分析 通过向量的垂直,向量的数量积得到∠FOP=30°,设双曲线另一个焦点为D,则在△POD中,利用余弦定理以及双曲线的定义,即可求出双曲线的离心率.
解答 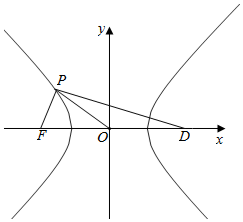 解:∵$\overrightarrow{OP}•\overrightarrow{PF}=0$,∴$\overrightarrow{OP}⊥\overrightarrow{PF}$,
解:∵$\overrightarrow{OP}•\overrightarrow{PF}=0$,∴$\overrightarrow{OP}⊥\overrightarrow{PF}$,
∴4$\overrightarrow{OP}$•$\overrightarrow{OF}$=4|$\overrightarrow{OP}$|•|$\overrightarrow{OF}$|cos<$\overrightarrow{OP}$,$\overrightarrow{OF}$>=4|$\overrightarrow{OP}$|•|$\overrightarrow{OF}$|•$\frac{|OP|}{|OF|}$=4|OP|2=3${\overrightarrow{OF}^2}$=3c2,
则|OP|=$\frac{\sqrt{3}}{2}$ c,
则cos∠FOP=$\frac{|OP|}{|OF|}$=$\frac{\frac{\sqrt{3}}{2}c}{c}$=$\frac{\sqrt{3}}{2}$,
则∠FOP=30°,
则|PF|=$\frac{1}{2}$c
设双曲线另一个焦点为D,则在△POD中,
由余弦定理可得|PD|2=|OP|2+|OD|2-2|OP||OD|cos150°=$\frac{3}{4}$c2+c2+2×$\frac{\sqrt{3}}{2}$ c•c•$\frac{\sqrt{3}}{2}$=$\frac{13}{4}$c2,
则|PD|=$\frac{\sqrt{13}}{2}$c,
∵|PF|=$\frac{1}{2}$c,
∴由双曲线定义得|PD|-|PF|=2a,
即$\frac{\sqrt{13}}{2}$c-$\frac{1}{2}$c=2a,
则离心率e=$\frac{c}{a}$=$\frac{4}{\sqrt{13}-1}$=$\frac{4(\sqrt{13}+1)}{13-1}$=$\frac{4(\sqrt{13}+1)}{12}$=$\frac{{\sqrt{13}+1}}{3}$,
故选:A.
点评 本题主要考查双曲线离心率的计算,根据向量垂直以及余弦定理结合双曲线的定义建立方程关系是解决本题的关键.考查学生的运算和转化能力.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{125π}{6}$ | B. | $\frac{125π}{24}$ | C. | 25π | D. | $\frac{500π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b<d | B. | c<d<a<b | C. | b<d<c<a | D. | d<b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | -1+2i | C. | 1-2i,-1+2i | D. | 1+2i,1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com