
分析 (1)由题意画出图象设BC=x,由条件和勾股定理求出BD、AB,由直角三角形的正弦函数求出sin∠BAC,在△ABD中由正弦定理列出方程求出x的值;
(2)设BC=x,由条件和勾股定理求出BD、AB,由直角三角形的正弦函数求出sin∠BAC,在△ABD中由正弦定理列出方程化简后,表示出sin∠ABD,化简后利用基本定理求出sin∠ABD的范围,由∠ABD的范围和正弦函数的性质求出∠ABD的最大值.
解答 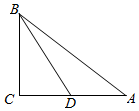 解:(1)如图所示:设BC=x,
解:(1)如图所示:设BC=x,
∵C=$\frac{π}{2}$,AC=2,D为AC中点,∴DC=AD=1,
且AB=$\sqrt{{x}^{2}+4}$,BD=$\sqrt{{x}^{2}+1}$,
∴sin∠BAC=$\frac{BC}{AB}$=$\frac{x}{\sqrt{{x}^{2}+4}}$,
∵sin∠ABD=$\frac{1}{3}$,∴在△ABD中,由正弦定理得$\frac{BD}{sin∠BAC}=\frac{AD}{sin∠DBA}$,
则$\frac{\sqrt{{x}^{2}+1}}{\frac{x}{\sqrt{{x}^{2}+4}}}=\frac{1}{\frac{1}{3}}$,即3$\frac{x}{\sqrt{{x}^{2}+4}}$=$\sqrt{{x}^{2}+1}$,
化简得x4-4x2+4=0,解得x2=2,即x=$\sqrt{2}$,
∴BD=$\sqrt{2}$;
(2)设BC=x,
∵C=$\frac{π}{2}$,AC=2,D为AC上靠近点C的三等分点,∴DC=$\frac{2}{3}$、AD=$\frac{4}{3}$,
且AB=$\sqrt{{x}^{2}+4}$,BD=$\sqrt{{x}^{2}+\frac{4}{9}}$,
∴sin∠BAC=$\frac{BC}{AB}$=$\frac{x}{\sqrt{{x}^{2}+4}}$,
在△ABD中,由正弦定理得$\frac{BD}{sin∠BAC}=\frac{AD}{sin∠DBA}$,则$\frac{\sqrt{{x}^{2}+\frac{4}{9}}}{\frac{x}{\sqrt{{x}^{2}+4}}}=\frac{\frac{4}{3}}{sin∠ABD}$,
即sin∠ABD=$\frac{4}{3}•\frac{\frac{x}{\sqrt{{x}^{2}+4}}}{\sqrt{{x}^{2}+\frac{4}{9}}}$=$\frac{4}{3}•\frac{x}{\sqrt{{(x}^{2}+4)({x}^{2}+\frac{4}{9})}}$=$\frac{4}{3}•\frac{x}{\sqrt{{x}^{4}+\frac{40}{9}{x}^{2}+\frac{16}{9}}}$
=$\frac{4}{3}•\frac{1}{\sqrt{{x}^{2}+\frac{16}{9{x}^{2}}+\frac{40}{9}}}$$≤\frac{4}{3}•\frac{1}{\sqrt{2×\frac{4}{3}+\frac{40}{9}}}$=$\frac{4}{3}×\frac{1}{\frac{8}{3}}$=$\frac{1}{2}$,
当且仅当${x}^{2}=\frac{16}{9{x}^{2}}$时取等号,
∴$sin∠ABD≤\frac{1}{2}$,
∵∠ABD是锐角,∴∠ABD的最大值是$\frac{π}{6}$,
故答案为:$\sqrt{2};\frac{π}{6}$.
点评 本题考查正弦定理、勾股定理,求角转化为求角的某个三角函数值,以及基本不等式求最值问题等,考查化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{13}+1}}{3}$ | B. | $\frac{{\sqrt{7}+\sqrt{3}}}{3}$ | C. | $\sqrt{7}$+$\sqrt{3}$ | D. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 中学成绩不优秀 | 中学成绩优秀 | 总计 | |
| 小学成绩优秀 | 5 | 20 | 25 |
| 小学成绩不优秀 | 10 | 5 | 15 |
| 合计 | 15 | 25 | 40 |
| A. | 在犯错误的概率不超过0.1的前提下,认为“小学成绩与中学成绩无关” | |
| B. | 在犯错误的概率不超过0.1的前提下,认为“小学成绩与中学成绩有关” | |
| C. | 在犯错误的概率不超过0.01的前提下,认为“小学成绩与中学成绩无关” | |
| D. | 在犯错误的概率不超过0.01的前提下,认为“小学成绩与中学成绩有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{1-\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}-1}}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com