
| A. | (-∞,1] | B. | (-∞,1) | C. | (-∞,2] | D. | (-∞,2) |
分析 求f′(x)=6x2-6mx+6,根据题意可知f′(x)≥0在(1,+∞)上恒成立,可设g(x)=6x2-6mx+6,法一:讨论△的取值,从而判断g(x)≥0是否在(1,+∞)上恒成立:△≤0时,容易求出-2≤m≤2,显然满足g(x)≥0;△<0时,得到关于m的不等式组,这样求出m的范围,和前面求出的m范围求并集即可,法二:分离参数,此时求出m的范围即可.
解答 解:f′(x)=6x2-6mx+6;
由已知条件知x∈(1,+∞)时,f′(x)≥0恒成立;
设g(x)=6x2-6mx+6,则g(x)≥0在(1,+∞)上恒成立;
法一:(1)若△=36(m2-4)≤0,即-2≤m≤2,满足g(x)≥0在(1,+∞)上恒成立;
(2)若△=36(m2-4)>0,即m<-2,或m>2,
则需:$\left\{\begin{array}{l}{\frac{m}{2}<1}\\{g(1)=6-6m≥0}\end{array}\right.$解得m≤2;
∴m<-2,
∴综上得m≤2,
∴实数m的取值范围是(-∞,2];
法二:问题转化为m≤x+$\frac{1}{x}$在(1,+∞)恒成立,
而函数y=x+$\frac{1}{x}$≥2,
故m≤2;
故选:C.
点评 考查函数单调性和函数导数符号的关系,熟练掌握二次函数的图象,以及判别式△的取值情况和二次函数取值的关系.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
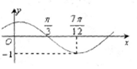 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com