
【题目】在平面直角坐标系![]() 中,已知椭圆C:
中,已知椭圆C:![]() (
(![]() >
>![]() >0)的右焦点为F(1,0),且过点(1,
>0)的右焦点为F(1,0),且过点(1,![]() ),过点F且不与
),过点F且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆C交于A,B两点,点P在椭圆上,且满足
与椭圆C交于A,B两点,点P在椭圆上,且满足![]() .
.
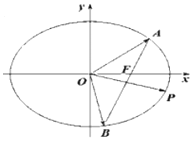
(1)求椭圆C的标准方程;
(2)若![]() ,求直线AB的方程.
,求直线AB的方程.
科目:高中数学 来源: 题型:
【题目】图1是由正方形![]() ,直角梯形
,直角梯形![]() ,三角形
,三角形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,将其沿
,将其沿![]() ,
,![]() 折起使得
折起使得![]() 与
与![]() 重合,连接
重合,连接![]() ,如图2.
,如图2.
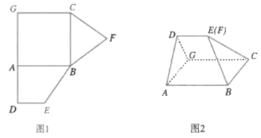
(1)证明:图2中的![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面ABCD,底面ABCD是等腰梯形,
平面ABCD,底面ABCD是等腰梯形,![]() ,
,![]() .
.
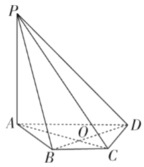
(1)证明:![]() 平面PAC;
平面PAC;
(2)若![]() ,
,![]() ,设
,设![]() ,且
,且![]() ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 分别为菱形
分别为菱形![]() 的边
的边![]() 的中点,将菱形沿对角线
的中点,将菱形沿对角线![]() 折起,使点
折起,使点![]() 不在平面
不在平面![]() 内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
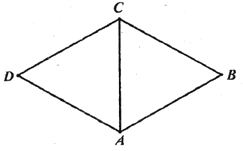
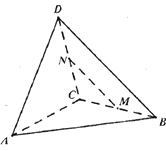
①![]() 平面
平面![]() ;②异面直线
;②异面直线![]() 与
与![]() 所成的角为定值;③在二面角
所成的角为定值;③在二面角![]() 逐渐渐变小的过程中,三棱锥
逐渐渐变小的过程中,三棱锥![]() 的外接球半径先变小后变大;④若存在某个位程,使得直线
的外接球半径先变小后变大;④若存在某个位程,使得直线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2),动点M到点A的距离比动点M到直线y=﹣1的距离大1,动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)设函数![]() 的导函数是
的导函数是![]() ,若不等式
,若不等式![]() 对于任意的实数
对于任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,
,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欲设计如图所示的平面图形,它由上、下两部分组成,其中上部分是弓形(圆心为![]() ,半径为
,半径为![]() ,
,![]() ,
,![]() ),下部分是矩形
),下部分是矩形![]() .
.
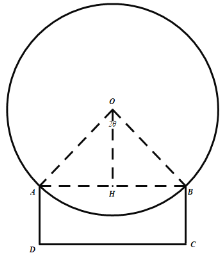
(1)若![]() ,求该平面图形的周长的最大值;
,求该平面图形的周长的最大值;
(2)若![]() ,试确定
,试确定![]() 的值,使得该平面图形的面积最大.
的值,使得该平面图形的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,平面
所在平面,平面![]() 平面
平面![]() ,且
,且![]() ,且
,且![]() .
.

(1)设点![]() 为棱
为棱![]() 中点,在面
中点,在面![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请证明,若不存在,说明理由;
?若存在,请证明,若不存在,说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从2011年到2018年参加“北约”,“华约”考试而获得加分的学生(每位学生只能参加“北约”,“华约”一种考试)人数可以通过以下表格反映出来.(为了方便计算,将2011年编号为1,2012年编号为2,依此类推……)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数y | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
(1)据悉,该校2018年获得加分的6位同学中,有1位获得加20分,2位获得加15分,3位获得加10分,从该6位同学中任取两位,记该两位同学获得的加分之和为X,求X的分布列及期望.
(2)根据最近五年的数据,利用最小二乘法求出y与x之间的线性回归方程,并用以预测该校2019年参加“北约”,“华约”考试而获得加分的学生人数.(结果要求四舍五入至个位)
参考公式: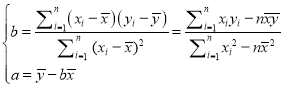
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com