
【题目】已知某品牌手机公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元.设公司一年内共生产该款手机x万部并全部销售完,每万部的销售收入为R(x)万美元,且R(x)=  .
.
(1)写出年利润f(x)(万美元)关于年产量x(万部)的函数解析式;
(2)当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大?并求出最大利润.
【答案】
(1)解:利用利润等于收入减去成本,可得
当0<x≤40时,f(x)=xR(x)﹣(16x+40)=﹣6x2+384x﹣40;
当x>40时,f(x)=xR(x)﹣(16x+40)=﹣ ![]() ﹣16x+7960
﹣16x+7960
∴f(x)= 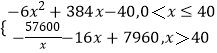 ;
;
(2)解:当0<x≤40时,f(x)=﹣6x2+384x﹣40=﹣6(x﹣32)2+6104,
∴x=32时,f(x)max=f(32)=6104;
当x>40时,f(x)=xR(x)﹣(16x+40)=﹣ ![]() ﹣16x+7960≤﹣2
﹣16x+7960≤﹣2 ![]() +7960,
+7960,
当且仅当 ![]() =16x,即x=60时,f(x)max=f(60)=7768
=16x,即x=60时,f(x)max=f(60)=7768
∵7768>6103
∴x=60时,f(x)的最大值为7768万美元
【解析】(1)利用利润等于收入减去成本,可得分段函数解析式;(2)分段求出函数的最大值,比较可得结论.


科目:高中数学 来源: 题型:
【题目】设f(x)=1﹣![]() ,求解:(1)f(x)的值域;(2)证明f(x)为R上的增函数. .
,求解:(1)f(x)的值域;(2)证明f(x)为R上的增函数. .
(1)求f(x)的值域;
(2)证明f(x)为R上的增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知g(x)=sin2x,将g(x)的图象向左平移 ![]() 个单位长度,再将图象上各点的横坐标缩短到原来的
个单位长度,再将图象上各点的横坐标缩短到原来的 ![]() ,得到函数f(x)的图象,则( )
,得到函数f(x)的图象,则( )
A.![]()
B.![]() ??
??
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ) ![]() 在某一个周期内的图象时,列表并填入了部分数据,如表:
在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
f(x)=Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将如表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
(3)求当 ![]() 时,函数y=g(x)的值域.
时,函数y=g(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com