
已知抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)动直线 恒过点
恒过点 与抛物线
与抛物线 交于A、B两点,与
交于A、B两点,与 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
(Ⅰ) (Ⅱ)存在三线段MA、MC、MB的长成等比数列.
(Ⅱ)存在三线段MA、MC、MB的长成等比数列.
【解析】
试题分析:(Ⅰ)∵椭圆方程为: ,∴
,∴ ,
,
所以 ,椭圆的右焦点为(1 , 0),抛物线的焦点为(
,椭圆的右焦点为(1 , 0),抛物线的焦点为( ,0),所以
,0),所以 =2,
=2,
则抛物线的方程为
(Ⅱ)设直线l: ,则C(-
,则C(- ,0),
,0),
由 得
得 ,
,
因为△= ,所以k<1,
,所以k<1,
设A(x1,y1),B(x2,y2),则 ,
, ,
,
所以由弦长公式得: ,
, ,
, ,
,
 ,
,
通过观察得: =(
=( )·
)· =(
=( )·
)· =
= .
.
若 =
= ,则
,则 ,不满足题目要求.
,不满足题目要求.
所以存在三线段MA、MC、MB的长成等比数列.
考点:直线与圆锥曲线的综合问题;抛物线的标准方程.
点评:本题考查椭圆的方程与性质,考查抛物线的方程,考查直线与武平县的位置关系,考查韦达定理的运用,考查等比数列的判定,属于中档题.


科目:高中数学 来源: 题型:
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 9y2 |
| 8 |
|
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| r1 |
| r2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2m |
| 3 |
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| 2m |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市浦东新区高三4月高考预测(二模)理科数学试卷(解析版) 题型:解答题
(1)设椭圆 :
: 与双曲线
与双曲线 :
: 有相同的焦点
有相同的焦点 ,
, 是椭圆
是椭圆 与双曲线
与双曲线 的公共点,且
的公共点,且 的周长为
的周长为 ,求椭圆
,求椭圆 的方程;
的方程;
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.
(2)如图,已知“盾圆 ”的方程为
”的方程为 .设“盾圆
.设“盾圆 ”上的任意一点
”上的任意一点 到
到 的距离为
的距离为 ,
, 到直线
到直线 的距离为
的距离为 ,求证:
,求证: 为定值;
为定值;

(3)由抛物线弧 :
: (
(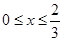 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧 :
: (
( )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”.设过点
”.设过点 的直线与“盾圆
的直线与“盾圆 ”交于
”交于 两点,
两点, ,
,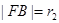 且
且 (
( ),试用
),试用 表示
表示 ;并求
;并求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)第一题满分4分,第二题满分6分,第三题满分8分.
已知椭圆![]() 的长轴长是焦距的两倍,其左、右焦点依次为
的长轴长是焦距的两倍,其左、右焦点依次为![]() 、
、![]() ,抛物线
,抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,椭圆
,椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,直线![]() 过焦点
过焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程;
的方程;
(3)由抛物线弧![]()
![]() 和椭圆弧
和椭圆弧![]()
![]()
(![]() )合成的曲线叫“抛椭圆”,是否存在以原点
)合成的曲线叫“抛椭圆”,是否存在以原点![]() 为直角顶点,另两个顶点
为直角顶点,另两个顶点![]() 落在“抛椭圆”上的等腰直角三角形
落在“抛椭圆”上的等腰直角三角形![]() ,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)第一题满分4分,第二题满分6分,第三题满分8分.
已知椭圆![]() 的长轴长是焦距的两倍,其左、右焦点依次为
的长轴长是焦距的两倍,其左、右焦点依次为![]() 、
、![]() ,抛物线
,抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,椭圆
,椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,直线![]() 过焦点
过焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程;
的方程;
(3)由抛物线弧![]()
![]() 和椭圆弧
和椭圆弧![]()
![]()
(![]() )合成的曲线叫“抛椭圆”,是否存在以原点
)合成的曲线叫“抛椭圆”,是否存在以原点![]() 为直角顶点,另两个顶点
为直角顶点,另两个顶点![]() 落在“抛椭圆”上的等腰直角三角形
落在“抛椭圆”上的等腰直角三角形![]() ,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com