Question

【题目】已知函数，；.

（1）求的最大值；

（2）若对，总存在使得成立，求的取值范围；

（3）证明不等式.

Answer 1

【答案】

【解析】

试题分析：

（1）对函数求导，，时，，当时，，函数单调递增，当时，，函数单调递减，所以当时，函数取得极大值，也是最大值，所以的最大值为；

（2）若对，总存在使得成立，则转化为，由（1）知，问题转化为求函数在区间上的最大值，对求导，，分类讨论，当时，函数在上恒成立，在上单调递增，只需满足，，解得，所以；当时，时，（舍），当时，在上恒成立，只需满足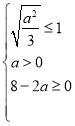，，解得，当，即时，在递减，递增，而，在为正，在为负，∴，当，而时，，不合题意，可以求出的取值范围。

（3）由（1）知：即， 取，∴，

∴，即∴，等号右端为等比数列求和。

试题解析：（1）∵，

∴，

∴当时，，时，，

∴，∴的最大值为.

（2），使得成立，等价于

由（1）知，，当时，在时恒为正，满足题意.

当时，，令，解得，

∴在上单调递减，在上单调递增，

若，即时，，∴，∴.

若，即时，在递减，递增，而，在为正，在为负，∴，

当，而时，，不合题意，

综上的取值范围为.

（3）由（1）知：即，

取，∴，∴，即

∴

.