
ЎҫМвДҝЎҝДіі¬КРФЪҪЪИХЖЪјдҪшРРУРҪұҙЩПъЈ¬·ІФЪёГі¬КР№әОпВъ![]() ФӘөД№ЛҝНЈ¬Ҫ«»сөГТ»ҙОГюҪұ»ъ»бЈ¬№жФтИзПВЈәТ»ёцҙьЧУЧ°УР
ФӘөД№ЛҝНЈ¬Ҫ«»сөГТ»ҙОГюҪұ»ъ»бЈ¬№жФтИзПВЈәТ»ёцҙьЧУЧ°УР![]() Ц»РОЧҙәНҙуРЎҫщПаН¬өДІЈБ§ЗтЈ¬ЖдЦРБҪЦ»КЗәмЙ«Ј¬ИэЦ»КЗВМЙ«Ј¬№ЛҝНҙУҙьЧУЦРТ»ҙОГюіцБҪЦ»ЗтЈ¬ИфБҪЦ»Зт¶јКЗәмЙ«Ј¬ФтҪұАш
Ц»РОЧҙәНҙуРЎҫщПаН¬өДІЈБ§ЗтЈ¬ЖдЦРБҪЦ»КЗәмЙ«Ј¬ИэЦ»КЗВМЙ«Ј¬№ЛҝНҙУҙьЧУЦРТ»ҙОГюіцБҪЦ»ЗтЈ¬ИфБҪЦ»Зт¶јКЗәмЙ«Ј¬ФтҪұАш![]() ФӘЈ»№ІБҪЦ»Зт¶јКЗВМЙ«Ј¬ФтҪұАш
ФӘЈ»№ІБҪЦ»Зт¶јКЗВМЙ«Ј¬ФтҪұАш![]() ФӘЈ»ИфБҪЦ»ЗтСХЙ«І»Н¬Ј¬ФтІ»ҪұАшЈ®
ФӘЈ»ИфБҪЦ»ЗтСХЙ«І»Н¬Ј¬ФтІ»ҪұАшЈ®
ЈЁ1Ј©ЗуТ»Гы№ЛҝНФЪТ»ҙОГюҪұ»о¶ҜЦР»сөГ![]() ФӘөДёЕВКЈ»
ФӘөДёЕВКЈ»
ЈЁ2Ј©јЗ![]() ОӘБҪГы№ЛҝНІОУлёГГюҪұ»о¶Ҝ»сөГөДҪұАшЧЬКэ¶оЈ¬ЗуЛж»ъұдБҝ
ОӘБҪГы№ЛҝНІОУлёГГюҪұ»о¶Ҝ»сөГөДҪұАшЧЬКэ¶оЈ¬ЗуЛж»ъұдБҝ![]() өД·ЦІјБРәНКэС§ЖЪНыЈ®
өД·ЦІјБРәНКэС§ЖЪНыЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©јыҪвОц
Ј»ЈЁ2Ј©јыҪвОц
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭ№ЕөдёЕРНёЕВКјЖЛ㹫КҪҝЙЗуөГҪб№ыЈ»ЈЁ2Ј©·ЦұрЗуіцТ»Гы№ЛҝНГюЗтЦРҪұ![]() ФӘәНІ»ЦРҪұөДёЕВКЈ»И·¶Ё
ФӘәНІ»ЦРҪұөДёЕВКЈ»И·¶Ё![]() ЛщУРҝЙДЬөДИЎЦөОӘЈә
ЛщУРҝЙДЬөДИЎЦөОӘЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬·ЦұрјЖЛгГҝёцИЎЦө¶ФУҰөДёЕВКЈ¬ҙУ¶шөГөҪ·ЦІјБРЈ»АыУГКэС§ЖЪНыјЖЛ㹫КҪЗуҪвЖЪНыјҙҝЙ.
Ј¬·ЦұрјЖЛгГҝёцИЎЦө¶ФУҰөДёЕВКЈ¬ҙУ¶шөГөҪ·ЦІјБРЈ»АыУГКэС§ЖЪНыјЖЛ㹫КҪЗуҪвЖЪНыјҙҝЙ.
ЈЁ1Ј©јЗТ»Гы№ЛҝНГюЗтЦРҪұ![]() ФӘОӘКВјю
ФӘОӘКВјю![]()
ҙУҙьЦРГюіцБҪЦ»Зт№ІУРЈә![]() ЦЦИЎ·ЁЈ»ГюіцөДБҪЦ»ЗтҫщКЗәмЗт№ІУРЈә
ЦЦИЎ·ЁЈ»ГюіцөДБҪЦ»ЗтҫщКЗәмЗт№ІУРЈә![]() ЦЦИЎ·Ё
ЦЦИЎ·Ё
![]()
ЈЁ2Ј©јЗТ»Гы№ЛҝНГюЗтЦРҪұ![]() ФӘОӘКВјю
ФӘОӘКВјю![]() Ј¬І»ЦРҪұОӘКВјю
Ј¬І»ЦРҪұОӘКВјю![]()
ФтЈә![]() Ј¬
Ј¬![]()
УЙМвТвҝЙЦӘЈ¬![]() ЛщУРҝЙДЬөДИЎЦөОӘЈә
ЛщУРҝЙДЬөДИЎЦөОӘЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
Фт![]() Ј»
Ј»![]() Ј»
Ј»
![]() Ј»
Ј»![]() Ј»
Ј»
![]()
![]() Лж»ъұдБҝ
Лж»ъұдБҝ![]() өД·ЦІјБРОӘЈә
өД·ЦІјБРОӘЈә
|
|
|
|
|
|
|
|
|
|
|
|
![]()



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэf(x)ЈҪlnx©Ғx2+axЈ¬g(x)ЈҪex©ҒeЈ¬ЖдЦРaЈҫ0.
(1)ИфaЈҪ1Ј¬ЦӨГчЈәf(x)ЎЬ0Ј»
(2)УГmax{mЈ¬n}ұнКҫmәНnЦРөДҪПҙуЦөЈ¬ЙиәҜКэh(x)ЈҪmax{f(x)Ј¬g(x)}Ј¬МЦВЫәҜКэh(x)ФЪ(0Ј¬+ЎЮ)ЙПөДБгөгөДёцКэ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ№эНЦФІW:![]() өДЧуҪ№өг
өДЧуҪ№өг![]() ЧчЦұПЯ
ЧчЦұПЯ![]() Ҫ»НЦФІУЪ
Ҫ»НЦФІУЪ![]() БҪөгЈ¬ЖдЦР
БҪөгЈ¬ЖдЦР![]()
![]() Ј¬БнТ»Мх№э
Ј¬БнТ»Мх№э![]() өДЦұПЯ
өДЦұПЯ![]() Ҫ»НЦФІУЪ
Ҫ»НЦФІУЪ![]() БҪөгЈЁІ»Ул
БҪөгЈЁІ»Ул![]() ЦШәПЈ©Ј¬ЗТ
ЦШәПЈ©Ј¬ЗТ![]() өгІ»Улөг
өгІ»Улөг![]() ЦШәП.№э
ЦШәП.№э![]() Чч
Чч![]() ЦбөДҙ№ПЯ·ЦұрҪ»ЦұПЯ
ЦбөДҙ№ПЯ·ЦұрҪ»ЦұПЯ![]() Ј¬
Ј¬![]() УЪ
УЪ![]() ,
,![]() .
.
ЈЁўсЈ©Зу![]() өгЧшұкәНЦұПЯ
өгЧшұкәНЦұПЯ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁўтЈ©ЗуЦӨЈә![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈ200ГыС§ЙъөДКэС§ЖЪЦРҝјКФіЙјЁЖөВК·ЦІјЦұ·ҪНјИзНјЛщКҫЈ¬ЖдЦРіЙјЁ·ЦЧйЗшјдКЗ![]()
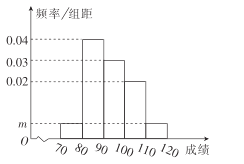
ЈЁ1Ј©ЗуНјЦР![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ёщҫЭЖөВК·ЦІјЦұ·ҪНјЈ¬№АјЖХв200ГыС§ЙъөДЖҪҫщ·ЦЈ»
ЈЁ3Ј©ИфХв200ГыС§ЙъөДКэС§іЙјЁЦРЈ¬ДіР©·ЦКэ¶ОөДИЛКэ![]() УлУўУпіЙјЁПаУҰ·ЦКэ¶ОөДИЛКэ
УлУўУпіЙјЁПаУҰ·ЦКэ¶ОөДИЛКэ![]() Ц®ұИИзұнЛщКҫЈ¬ЗуУўУпіЙјЁФЪ
Ц®ұИИзұнЛщКҫЈ¬ЗуУўУпіЙјЁФЪ![]() өДИЛКэ.
өДИЛКэ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘПВБРГьМвЈә
ўЩ»Ш№йЦұПЯ![]() әг№эСщұҫөгөДЦРРД
әг№эСщұҫөгөДЦРРД![]() Ј¬ЗТЦБЙЩ№эТ»ёцСщұҫөгЈ»
Ј¬ЗТЦБЙЩ№эТ»ёцСщұҫөгЈ»
ўЪБҪёцұдБҝПа№ШРФФҪЗҝЈ¬ФтПа№ШПөКэrҫНФҪҪУҪьУЪ1Ј»
ўЫҪ«Т»ЧйКэҫЭөДГҝёцКэҫЭ¶јјУТ»ёцПаН¬өДіЈКэәуЈ¬·ҪІоІ»ұдЈ»
ўЬФЪ»Ш№йЦұПЯ·ҪіМ![]() ЦРЈ¬өұҪвКНұдБҝxФцјУТ»ёцөҘО»КұЈ¬ФӨұЁұдБҝ
ЦРЈ¬өұҪвКНұдБҝxФцјУТ»ёцөҘО»КұЈ¬ФӨұЁұдБҝ![]() ЖҪҫщјхЙЩ0.5Ј»
ЖҪҫщјхЙЩ0.5Ј»
ўЭФЪПЯРФ»Ш№йДЈРНЦРЈ¬Па№ШЦёКэ![]() ұнКҫҪвКНұдБҝ
ұнКҫҪвКНұдБҝ![]() ¶ФУЪФӨұЁұдБҝ
¶ФУЪФӨұЁұдБҝ![]() өД№ұПЧВКЈ¬
өД№ұПЧВКЈ¬![]() ФҪҪУҪьУЪ1Ј¬ұнКҫ»Ш№йР§№ыФҪәГЈ»
ФҪҪУҪьУЪ1Ј¬ұнКҫ»Ш№йР§№ыФҪәГЈ»
ўЮ¶Ф·ЦАаұдБҝ![]() Ул
Ул![]() Ј¬ЛьГЗөДЛж»ъұдБҝ
Ј¬ЛьГЗөДЛж»ъұдБҝ![]() өД№ЫІвЦө
өД№ЫІвЦө![]() АҙЛөЈ¬
АҙЛөЈ¬ ![]() ФҪРЎЈ¬Ў°
ФҪРЎЈ¬Ў°![]() Ул
Ул![]() УР№ШПөЎұөД°СОХіМ¶ИФҪҙуЈ®
УР№ШПөЎұөД°СОХіМ¶ИФҪҙуЈ®
ўЯБҪёцДЈРНЦРІРІоЖҪ·ҪәНФҪРЎөДДЈРНДвәПөДР§№ыФҪәГ.
ФтХэИ·ГьМвөДёцКэКЗЈЁ Ј©
A. 3 B. 4 C. 5 D. 6
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() өДҪ№өгФЪ
өДҪ№өгФЪ![]() ЦбЙПЈ¬ЗТНЦФІ
ЦбЙПЈ¬ЗТНЦФІ![]() өДҪ№ҫаОӘ2Ј®
өДҪ№ҫаОӘ2Ј®
ЈЁўсЈ©ЗуНЦФІ![]() өДұкЧј·ҪіМЈ»
өДұкЧј·ҪіМЈ»
ЈЁўтЈ©№эөг![]() өДЦұПЯ
өДЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() Ҫ»УЪБҪөг
Ҫ»УЪБҪөг![]() Ј¬№э
Ј¬№э![]() Чч
Чч![]() ЦбЗТУлНЦФІ
ЦбЗТУлНЦФІ![]() Ҫ»УЪБнТ»өг
Ҫ»УЪБнТ»өг![]() Ј¬
Ј¬ ![]() ОӘНЦФІ
ОӘНЦФІ![]() өДУТҪ№өгЈ¬ЗуЦӨЈәИэөг
өДУТҪ№өгЈ¬ЗуЦӨЈәИэөг![]() ФЪН¬Т»МхЦұПЯЙПЈ®
ФЪН¬Т»МхЦұПЯЙПЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ФЪИэАвЧ¶![]() ЦРЈ¬
ЦРЈ¬![]() КЗұЯіӨОӘ4өДХэИэҪЗРОЈ¬ЖҪГж
КЗұЯіӨОӘ4өДХэИэҪЗРОЈ¬ЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј¬SA=SC=
Ј¬SA=SC=![]() Ј¬MЈ¬N·ЦұрОӘABЈ¬SBөДЦРөг.
Ј¬MЈ¬N·ЦұрОӘABЈ¬SBөДЦРөг.
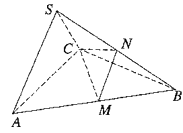
ЈЁ1Ј©ЗуЦӨЈәACЎНSBЈ»
ЈЁ2Ј©Зу¶юГжҪЗNЈӯCMЈӯBөДУаПТЦөЈ»
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com