
分析 (Ⅰ)由题意可得$e=\frac{{\sqrt{2}}}{2}$,c=1,a2=b2+c2,联立解出即可得出.
(Ⅱ)当直线l的斜率为0时,不成立.于是可设直线l的方程为:my=x-1,设A(x1,y1),B(x2,y2),与椭圆方程联立可得:(m2+2)y2+2my-1=0,由|FA|=λ|FB|,可得y1=-λy2,再利用根与系数的关系代入可得:$λ+\frac{1}{λ}$-2=$\frac{4{m}^{2}}{{m}^{2}+2}$,由1≤λ≤2,可得0≤${m^2}≤\frac{2}{7}$,利用AB边上的中线长为$\frac{1}{2}|\overrightarrow{TB}+\overrightarrow{TA}|$=$\frac{1}{2}\sqrt{({x}_{1}+{x}_{2}-4)^{2}+({y}_{1}+{y}_{2})^{2}}$,及其二次函数的单调性即可得出.
解答 解:(Ⅰ)∵$e=\frac{{\sqrt{2}}}{2}$,c=1,a2=b2+c2,
∴$a=\sqrt{2},c=1$=b,
∴椭圆C的方程为:$\frac{x^2}{2}+{y^2}=1$.
(Ⅱ)当直线l的斜率为0时,显然不成立.因此可设直线l的方程为:my=x-1,设A(x1,y1),B(x2,y2),
直线l的方程与椭圆方程联立可得:(m2+2)y2+2my-1=0,
∴${y_1}+{y_2}=\frac{-2m}{{{m^2}+2}}$,${y_1}{y_2}=\frac{-1}{{{m^2}+2}}$,
由|FA|=λ|FB|,可得y1=-λy2,
∵$-λ+\frac{1}{-λ}=\frac{y_1}{y_2}+\frac{y_2}{y_1}$,
∴$-λ+\frac{1}{-λ}+2=\frac{{{{({y_1}+{y_2})}^2}}}{{{y_1}{y_2}}}=\frac{{-4{m^2}}}{{{m^2}+2}}$,
∴$λ+\frac{1}{λ}$-2=$\frac{4{m}^{2}}{{m}^{2}+2}$,
∵1≤λ≤2,∴$λ+\frac{1}{λ}$∈$[2,\frac{5}{2}]$,
∴0≤${m^2}≤\frac{2}{7}$,
又AB边上的中线长为$\frac{1}{2}|\overrightarrow{TB}+\overrightarrow{TA}|$=$\frac{1}{2}\sqrt{({x}_{1}+{x}_{2}-4)^{2}+({y}_{1}+{y}_{2})^{2}}$=$\sqrt{\frac{4{m}^{4}+9{m}^{2}+4}{({m}^{2}+2)^{2}}}$=$\sqrt{\frac{2}{{{{({m^2}+2)}^2}}}-\frac{7}{{{m^2}+2}}+4}$,
∵0≤${m^2}≤\frac{2}{7}$,∴$\frac{1}{{m}^{2}+2}$=t∈$[\frac{7}{16},\frac{1}{2}]$.
∴f(t)=2t2-7t+4=2$(t-\frac{7}{4})^{2}$-$\frac{17}{8}$∈$[1,\frac{169}{128}]$.
∴$\sqrt{f(t)}$$∈[1,\frac{{13\sqrt{2}}}{16}]$.
∴△ABT中AB边上中线长的取值范围是$[1,\frac{13\sqrt{2}}{16}]$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、向量数量积运算性质、一元二次方程的根与系数的关系、二次函数的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+y2=1 | B. | (x+2)2+y2=1 | C. | (x-2)2+y2=4 | D. | x2+(y-2)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
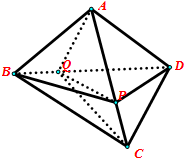 如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )
如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )| A. | 22 | B. | 34 | C. | 32 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-$\sqrt{2}$ | B. | 3+2$\sqrt{2}$ | C. | 3+$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x0)=0 | B. | f′(x0)<0 | ||
| C. | f′(x0)=0且f″(x0)<0 | D. | f′(x0)或f′(x0)不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com