
随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算,统计量K2=4.762,参照附表,得到的正确结论是( ).
A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:解答题
△ABC中内角A,B,C的对边分别为a,b,c,已知a=bcos C+csin B.
(1)求B;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:选择题
用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ).
A.243 B.252 C.261 D.279
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:解答题
如图,点P(0,-1)是椭圆C1: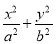 =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
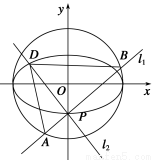
(1)求椭圆C1的方程;
(2)求△ABD面积取最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|·|CD|的值正确的是( ).
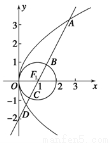
A.等于1 B.最小值是1 C.等于4 D.最大值是4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
设圆x2+y2=2的切线l与x轴的正半轴、y轴的正半轴分别交于点A,B,当|AB|取最小值时,切线l的方程为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
已知首项为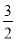 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-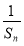 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com