
已知首项为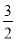 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-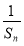 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
(1)(-1)n-1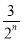 (2)
(2)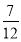
【解析】(1)解 设等比数列{an}的公比为q,因为S3+a3,S5+a5,S4+a4成等差数列,所以S5+a5-S3-a3=S4+a4-S5-a5,即4a5=a3,于是q2=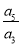 =
=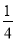 .
.
又{an}不是递减数列且a1=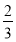 ,所以q=-
,所以q=-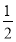 .
.
故等比数列{an}的通项公式为
an=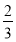 ×
×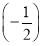 n-1=(-1)n-1
n-1=(-1)n-1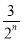 .
.
(2)由(1)得Sn=1-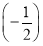 n=
n= ,当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=
,当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=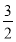 ,故0<Sn-
,故0<Sn-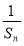 ≤S1-
≤S1-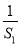 =
=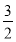 -
-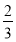 =
=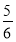
当n为偶数时,Sn随n的增大而增大,所以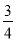 =S2≤Sn<1,故0>Sn-
=S2≤Sn<1,故0>Sn- ≥S2-
≥S2-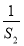 =
=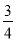 -
-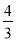 =-
=-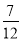 .
.
综上,对于n∈N*,总有-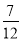 ≤Sn-
≤Sn-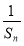 ≤
≤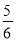 .
.
所以数列{Tn}最大项的值为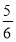 ,
,
最小项的值为-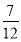 .
.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算,统计量K2=4.762,参照附表,得到的正确结论是( ).
A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知两条直线a,b与两个平面α,β,b⊥α,则下列命题中正确的是( ).
①若a∥α,则a⊥b;②若a⊥b,则a∥α;③若b⊥β,则α∥β;④若α⊥β,则b∥β.
A.①③ B.②④ C.①④ D.②③
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
在具有如图所示的正视图和俯视图的几何体中,体积最大的几何体的表面积为( ).
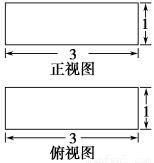
A.13 B.7+3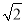 C.
C.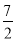 π D.14
π D.14
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:填空题
在正项数列{an}中,a1=2,an+1=2an+3×5n,则数列{an}的通项公式为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:解答题
已知直线l:y=x+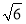 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: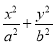 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=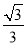 ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两条切线的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:解答题
如图,ABCD是块矩形硬纸板,其中AB=2AD,AD=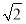 ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
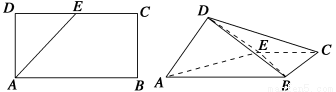
(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:选择题
若M为△ABC所在平面内一点,且满足(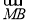 -
-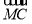 )·(
)·(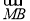 +
+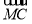 -2
-2 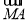 )=0,则△ABC为( ).
)=0,则△ABC为( ).
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com