
【题目】如图,在五面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
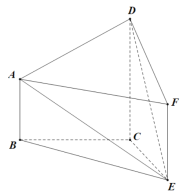
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据平行的传递性可得![]() ,再取
,再取![]() 中点为
中点为![]() ,连接
,连接![]() ,进而可得四边形
,进而可得四边形![]() 为平行四边形,再根据勾股定理证明
为平行四边形,再根据勾股定理证明![]() ,进而得到
,进而得到![]() 平面
平面![]() .
.
(2) 以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,再分别求解平面
,再分别求解平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,进而求得二面角的余弦值即可.
的法向量,进而求得二面角的余弦值即可.
(1)证明:因为![]() ,
,![]() ,
,
所以![]() .
.
取![]() 中点为
中点为![]() ,连接
,连接![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,且
,且![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
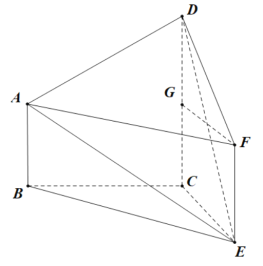
(2)由(1)知,![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
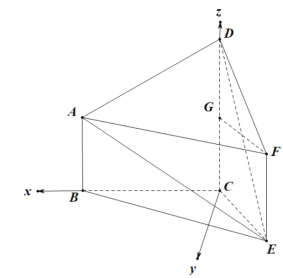
故以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、
![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() .
.
所以![]()
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则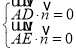 ,
,
所以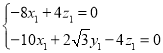 ,
,
取![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() ,
,
所以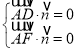 ,
,
所以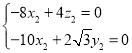 ,
,
取![]() ,则
,则![]() ,
,
所以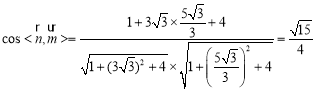 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏装机量 | 0.4 | 0.8 | 1.6 | 3.1 | 5.1 | 7.1 | 9.7 | 12.2 |
某位同学分别用两种模型:①![]() ,②
,②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() ):
):

经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立![]() 关于
关于![]() 的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:回归直线的斜率和截距的最小二乘估计公式分别为: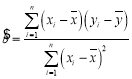 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法正确的是( )
A.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均减少2.3个单位
平均减少2.3个单位
B.两个具有线性相关关系的变量,当相关指数![]() 的值越接近于0,则这两个变量的相关性就越强
的值越接近于0,则这两个变量的相关性就越强
C.若两个变量的相关指数![]() ,则说明预报变量的差异有88%是由解释变量引起的
,则说明预报变量的差异有88%是由解释变量引起的
D.在回归直线方程![]() 中,相对于样本点
中,相对于样本点![]() 的残差为
的残差为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1为椭圆![]() 的左焦点,
的左焦点,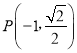 在椭圆上,PF1⊥x轴.
在椭圆上,PF1⊥x轴.
(1)求椭圆的方程:
(2)已知直线l与椭圆交于A,B两点,且坐标原点O到直线l的距离为![]() 的大小是否为定值?若是,求出该定值:若不是,请说明理由.
的大小是否为定值?若是,求出该定值:若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位年会进行抽奖活动,在抽奖箱里装有![]() 张印有“一等奖”的卡片,
张印有“一等奖”的卡片, ![]() 张印
张印
有“二等奖”的卡片, 3张印有“新年快乐”的卡片,抽中“一等奖”获奖![]() 元, 抽中“二等奖”获奖
元, 抽中“二等奖”获奖![]() 元,抽中“新年快乐”无奖金.
元,抽中“新年快乐”无奖金.
(1)单位员工小张参加抽奖活动,每次随机抽取一张卡片,抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记![]() 表示“小张恰好抽奖
表示“小张恰好抽奖![]() 次停止活动”,求
次停止活动”,求![]() 的值;
的值;
(2)若单位员工小王参加抽奖活动,一次随机抽取![]() 张卡片.
张卡片.
①![]() 记
记![]() 表示“小王参加抽奖活动中奖”,求
表示“小王参加抽奖活动中奖”,求![]() 的值;
的值;
②设![]() 表示“小王参加抽奖活动所获奖金数(单位:元)”,求
表示“小王参加抽奖活动所获奖金数(单位:元)”,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
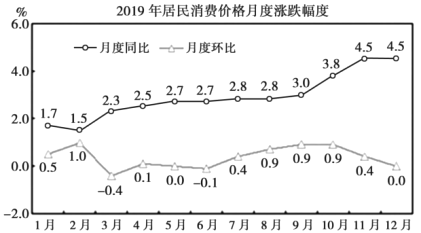
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com