
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏装机量 | 0.4 | 0.8 | 1.6 | 3.1 | 5.1 | 7.1 | 9.7 | 12.2 |
某位同学分别用两种模型:①![]() ,②
,②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() ):
):

经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立![]() 关于
关于![]() 的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:回归直线的斜率和截距的最小二乘估计公式分别为: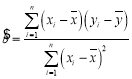 ,
,![]() .
.
【答案】(1)模型①的拟合效果相对较好;详见解析(2)回归方程为![]() ;预测该地区2020年新增光伏装机量为
;预测该地区2020年新增光伏装机量为![]() (兆瓦)
(兆瓦)
【解析】
(1)根据残差图的带状区域越窄,其模型的拟合效果越好即可判断;
(2)利用换元的思想,令![]() ,把非线性的回归方程
,把非线性的回归方程![]() 转化为线性的回归方程
转化为线性的回归方程![]() ,结合题中的数据和
,结合题中的数据和![]() 公式求出
公式求出![]() ,再由回归直线经过样本中心点
,再由回归直线经过样本中心点![]() ,求出
,求出![]() 即可求出回归方程;把
即可求出回归方程;把![]() 代入回归方程求出
代入回归方程求出![]() 即为所求的预测值.
即为所求的预测值.
(1)选择模型①.
理由如下:根据残差图可以看出,模型①的估计值和真实值相对比较接近,模型②的残差相对较大一些,所以模型①的拟合效果相对较好.
(2)由(1),知![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,令
,令![]() ,则
,则![]() .
.
由所给数据可得![]() ,
,
![]() ,
,
所以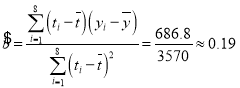 ,
,
由线性回归方程经过样本中心点![]() 可得,
可得,
![]() .
.
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
预测该地区2020年新增光伏装机量为![]() (兆瓦).
(兆瓦).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市数学教研室对全市2018级15000名的高中生的学业水平考试的数学成绩进行调研,随机选取了200名高中生的学业水平考试的数学成绩作为样本进行分析,将结果列成频率分布表如下:
数学成绩 | 频数 | 频率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合计 | 200 | 1 |
根据学业水平考试的数学成绩将成绩分为“优秀”、“合格”、“不合格”三个等级,其中成绩大于或等于80分的为“优秀”,成绩小于60分的为“不合格”,其余的成绩为“合格”.
(1)根据频率分布表中的数据,估计全市学业水平考试的数学成绩的众数、中位数(精确到0.1);
(2)市数学教研员从样本中又随机选取了![]() 名高中生的学业水平考试的数学成绩,如果这
名高中生的学业水平考试的数学成绩,如果这![]() 的最小值;
的最小值;
(3)估计全市2018级高中生学业水平考试“不合格”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: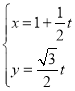 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点P是曲线
,设点P是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 、
、![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 、
、![]() 互相垂直.点M在
互相垂直.点M在![]() 上移动,点N在
上移动,点N在![]() 上移动,若
上移动,若![]() (
(![]() ).
).

(1)当a为何值时,![]() 的长最小;
的长最小;
(2)当![]() 长最小时,求面
长最小时,求面![]() 与面
与面![]() 所成的二面角α的余弦值.
所成的二面角α的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思为“今有水池1丈见方(即![]() 尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设
尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设![]() ,现有下述四个结论:
,现有下述四个结论:
①水深为12尺;②芦苇长为15尺;③![]() ;④
;④![]() .
.
其中所有正确结论的编号是( )
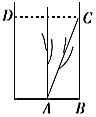
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com