Question

8．如图所示，一辆汽车从O点出发，沿海岸线一直线公路以100千米/小时的速度向东匀速行驶，汽车开动时，在距O点500千米，且与海岸线距离400千米的海面上M点处有一艘快艇与汽车同时出发，要把一件重要物品送给这辆汽车司机，该快艇至少以多大的速度行驶，才能将物品送到司机手中？并求出此时快艇行驶的方向．（参考数据：cos60°25′=$\frac{2}{5}$，cos53°08′=$\frac{3}{5}$，cos36°52′=$\frac{4}{5}$）

Answer 1

分析 设快艇从M处以v千米/小时的速度出发，沿MN方向航行，1小时后在N点与汽车相遇，MQ为M点到ON的距离，设∠MON=α，由余弦定理，求出MN²=OM²+ON²-2OM•ON•cosα，利用二次函数的性质求出最值，得到结果即可．

解答 解：如图所示，设快艇从M处以v千米/小时的速度出发，沿MN方向航行，1小时后在N点与汽车相遇，MQ为M点到ON的距离，则MQ=400，在△MON中，MO=500，ON=100t，MN=vt，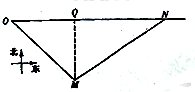
设∠MON=α，由题意知$sinα=\frac{4}{5}$，则$cosα=\frac{3}{5}$，…（2分）
由余弦定理，得MN²=OM²+ON²-2OM•ON•cosα，
即${v^2}{t^2}={500^2}+{100^2}{t^2}-2×500×100t×\frac{3}{5}$，…（4分）${v^2}=\frac{{{{500}^2}}}{t^2}-2×500×60×\frac{1}{t}+{100^2}={（\frac{500}{t}-60）^2}+{100^2}-{60^2}$…（6分）
当$\frac{500}{t}=60$，即$t=\frac{25}{3}$时，$v_{min}^2=6400$即快艇必须至少以80千米/小时速度行驶，
此时$MN=80×\frac{25}{3}=\frac{2000}{3}$，…（9分）
设∠NMQ=β，则$cosβ=\frac{MQ}{MN}=\frac{400}{2000}=-\frac{3}{5}$，…（11分）
故快艇的行驶方向北偏东53°08'…（12分）

点评 本题考查实际问题的应用，余弦定理以及二次函数的性质的应用，考查计算能力．