练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．一个几何体的三视图如图所示，则该几何体的表面积为（　　）
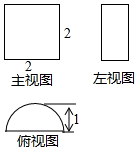
    A．3πB．4πC．2π+4D．3π+4

    分析 由已知中的三视图可得，该几何体是以俯视图为底面的半圆柱，底面半径为1，高为2，代入柱体表面积公式，可得答案．

    解答 解：由已知中的三视图可得，该几何体是以俯视图为底面的半圆柱，
    底面半径为1，高为2，
    故该几何体的表面积S=2×$\frac{1}{2}$π+（2+π）×2=3π+4，
    故选：D

    点评 本题考查的知识点是柱体的体积和表面积，简单几何体的三视图，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．如图所示，一辆汽车从O点出发，沿海岸线一直线公路以100千米/小时的速度向东匀速行驶，汽车开动时，在距O点500千米，且与海岸线距离400千米的海面上M点处有一艘快艇与汽车同时出发，要把一件重要物品送给这辆汽车司机，该快艇至少以多大的速度行驶，才能将物品送到司机手中？并求出此时快艇行驶的方向．（参考数据：cos60°25′=$\frac{2}{5}$，cos53°08′=$\frac{3}{5}$，cos36°52′=$\frac{4}{5}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

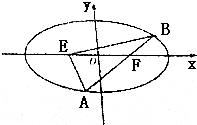    9．如图，已知椭圆C：$\frac{x^2}{9}+\frac{y^2}{b^2}$=1（0＜b＜3）的左右焦点分别为E、F，过点F的直线交椭圆于A，B两点，若$\overrightarrow{AF}$=2$\overrightarrow{FB}$，且$\overrightarrow{AE}$•$\overrightarrow{BE}$=16．
    （1）求椭圆C的方程；
    （2）设直线x=my+1与椭圆交于不同的两点P，Q，判断在x轴上是否存在定点N，使x轴平分∠PNQ，若存在，求出点N的坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若-1≤a-b≤1且2≤a+b≤4，则4a-2b的取值范围[-1，7]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设Sn是数列{an}的前n项和，且2Sn=3an-$\frac{2}{9}$，an≠0（n∈N*）；
    （1）求数列{an}的通项公式an和Sn；
    （2）若bn=$\frac{2n+3}{{（9{S_n}+1）n（n+1）}}$=$\frac{a}{{n•{3^{n-1}}}}$-$\frac{1}{{（n+1）•{3^n}}}$，（n∈N*），求bn和a值；
    （3）设Tn是数列{bn}的前n项和，求Tn的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数f（x）=$\sqrt{4+3x-{x}^{2}}$的单调递减区间是（　　）
    A．（-∞，$\frac{3}{2}$]B．[$\frac{3}{2}$，+∞）C．（-1，$\frac{3}{2}$]D．[$\frac{3}{2}$，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．有关正弦定理的叙述：
    ①正弦定理只适用于锐角三角形；
    ②正弦定理不适用于直角三角形；
    ③在某一确定的三角形中，各边与它的对角的正弦的比是定值；
    ④在△ABC中，sinA：sinB：sinC=a：b：c．其中正确的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知集合A={x|0＜ax-1≤5}，B={x|-$\frac{1}{2}$＜x≤2}，
    （Ⅰ）若a=1，求A∪B；
    （Ⅱ）若A∩B=∅且a≥0，求实数a的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数f（x）的导函数为f'（x），且满足f（x）=3xf'（1）+2lnx，则f'（1）=（　　）
    A．-eB．-1C．1D．e

    查看答案和解析>>

    同步练习册答案