
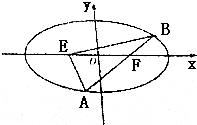
 如图,已知椭圆C:$\frac{x^2}{9}+\frac{y^2}{b^2}$=1(0<b<3)的左右焦点分别为E、F,过点F的直线交椭圆于A,B两点,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,且$\overrightarrow{AE}$•$\overrightarrow{BE}$=16.
如图,已知椭圆C:$\frac{x^2}{9}+\frac{y^2}{b^2}$=1(0<b<3)的左右焦点分别为E、F,过点F的直线交椭圆于A,B两点,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,且$\overrightarrow{AE}$•$\overrightarrow{BE}$=16.分析 (1)由题意可知:$\overrightarrow{AF}$=2$\overrightarrow{FB}$,则设|BF|=m,则|AF|=2m,由椭圆的定义可知:|BE|=6-m,|AE|=6-2m,由余弦定理可知cos∠AEB=$\frac{丨{AE丨}^{2}+丨BE{丨}^{2}-丨AB{丨}^{2}}{2丨AE丨•丨BE丨}$,$\overrightarrow{AE}$•$\overrightarrow{BE}$=丨$\overrightarrow{AE}$丨•丨$\overrightarrow{BE}$丨•$\frac{丨{AE丨}^{2}+丨BE{丨}^{2}-丨AB{丨}^{2}}{2丨AE丨•丨BE丨}$=16,即可求得m的值,丨EF丨=2$\sqrt{5}$,c=$\sqrt{5}$,b2=a2-c2=4,即可求得椭圆C的方程;
(2)由题意可知:设存在定点N(t,0),且设P(x1,y1),Q(x2,y2),kPN+kQN=0,由斜率公式可知:$\frac{y_1}{{{x_1}-t}}+\frac{y_2}{{{x_2}-t}}=1$,整理2my1y2+(1-t)(y1+y2)=0,将直线l的方程代入椭圆方程,由韦达定理可知:${y_1}+{y_2}=\frac{-8m}{{4{m^2}+9}},{y_1}{y_2}=\frac{-32}{{4{m^2}+9}}$,代入即可求得$2m•\frac{-32}{{4{m^2}+9}}+(1-t)\frac{-8m}{{4{m^2}+9}}=0⇒t=9$,故存在定点N(9,0).
解答 解:(1)由题意可知:$\overrightarrow{AF}$=2$\overrightarrow{FB}$,则丨$\overrightarrow{AF}$丨=2丨$\overrightarrow{FB}$丨,设|BF|=m,则|AF|=2m,
椭圆C:$\frac{x^2}{9}+\frac{y^2}{b^2}$=1(0<b<3),则焦点在x轴上,a=3,
由椭圆的定义可知:|AF|+|AE|=2a=6,|BF|+|BE|=2a=6,
∴|BE|=6-m,|AE|=6-2m,
在三角形AEB中,由余弦定理可知:cos∠AEB=$\frac{丨{AE丨}^{2}+丨BE{丨}^{2}-丨AB{丨}^{2}}{2丨AE丨•丨BE丨}$,
$\overrightarrow{AE}$•$\overrightarrow{BE}$=丨$\overrightarrow{AE}$丨•丨$\overrightarrow{BE}$丨•$\frac{丨{AE丨}^{2}+丨BE{丨}^{2}-丨AB{丨}^{2}}{2丨AE丨•丨BE丨}$,
由$\overrightarrow{AE}$•$\overrightarrow{BE}$=16,
解得:m=1,(3分)
∴三角形ABE是以角A为直角的直角三角形,
则丨EF丨=2$\sqrt{5}$,
∴c=$\sqrt{5}$,
故b2=a2-c2=4,(5分)
椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$; (6分)
(2)设存在定点N(t,0),且设P(x1,y1),Q(x2,y2),
由x轴平分∠PNQ,得kPN+kQN=0,(8分)
即$\frac{y_1}{{{x_1}-t}}+\frac{y_2}{{{x_2}-t}}=1$,而x1=my1+1,x2=my2+1,
则y1(my2+1-t)+y2(my1+1-t)=0,
即:2my1y2+(1-t)(y1+y2)=0,①,(9分)
$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,整理得:4(my+1)2+9y2-36=0,
即:(4m2+9)y2+8my-32=0,
由韦达定理可知:${y_1}+{y_2}=\frac{-8m}{{4{m^2}+9}},{y_1}{y_2}=\frac{-32}{{4{m^2}+9}}$,(10分)
代入①式得:$2m•\frac{-32}{{4{m^2}+9}}+(1-t)\frac{-8m}{{4{m^2}+9}}=0⇒t=9$,
故存在定点N(9,0)(12分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查余弦定理,向量的数量积及直线的斜率公式的综合运用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {l,2,3} | C. | {0} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{5}+1$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{100})$ | B. | $(\frac{1}{100},1)$ | C. | $(\frac{1}{100},100)$ | D. | (0,1)∪(100,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x+1 | B. | $y=\frac{x}{1-x}$ | C. | $y={log_{\frac{1}{2}}}(x-1)$ | D. | y=-(x-1)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com