
分析 根据$\overrightarrow{a}$+$\overrightarrow{b}$求出$\overrightarrow{b}$的坐标表示,利用$\overrightarrow{a}$∥$\overrightarrow{b}$求出x的值,再计算模长|$\overrightarrow{b}$|.
解答 解:向量$\overrightarrow{a}$=(3,1),$\overrightarrow{a}$+$\overrightarrow{b}$=(x,-1),
∴$\overrightarrow{b}$=$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{a}$=(x-3,-2);
又$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴(x-3)-3×(-2)=0,
解得x=-3,
∴$\overrightarrow{b}$=(-6,-2);
∴|$\overrightarrow{b}$|=$\sqrt{{(-6)}^{2}{+(-2)}^{2}}$=2$\sqrt{10}$.
故答案为:$2\sqrt{10}$.
点评 本题考查了平面向量的坐标运算与模长问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | (-e2+2e,0) | B. | (-e2+2e,+∞) | C. | (0,e2-2e) | D. | (-∞,-e2+2e) 第Ⅱ卷 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,一辆汽车从O点出发,沿海岸线一直线公路以100千米/小时的速度向东匀速行驶,汽车开动时,在距O点500千米,且与海岸线距离400千米的海面上M点处有一艘快艇与汽车同时出发,要把一件重要物品送给这辆汽车司机,该快艇至少以多大的速度行驶,才能将物品送到司机手中?并求出此时快艇行驶的方向.(参考数据:cos60°25′=$\frac{2}{5}$,cos53°08′=$\frac{3}{5}$,cos36°52′=$\frac{4}{5}$)
如图所示,一辆汽车从O点出发,沿海岸线一直线公路以100千米/小时的速度向东匀速行驶,汽车开动时,在距O点500千米,且与海岸线距离400千米的海面上M点处有一艘快艇与汽车同时出发,要把一件重要物品送给这辆汽车司机,该快艇至少以多大的速度行驶,才能将物品送到司机手中?并求出此时快艇行驶的方向.(参考数据:cos60°25′=$\frac{2}{5}$,cos53°08′=$\frac{3}{5}$,cos36°52′=$\frac{4}{5}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
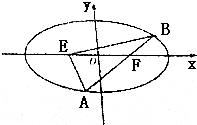 如图,已知椭圆C:$\frac{x^2}{9}+\frac{y^2}{b^2}$=1(0<b<3)的左右焦点分别为E、F,过点F的直线交椭圆于A,B两点,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,且$\overrightarrow{AE}$•$\overrightarrow{BE}$=16.
如图,已知椭圆C:$\frac{x^2}{9}+\frac{y^2}{b^2}$=1(0<b<3)的左右焦点分别为E、F,过点F的直线交椭圆于A,B两点,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,且$\overrightarrow{AE}$•$\overrightarrow{BE}$=16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com