Question

3．一个几何体的三视图如图所示，其中左视图为直角三角形，则该几何体的体积为$\frac{16\sqrt{2}}{3}$．

Answer 1

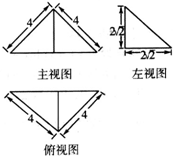
分析 根据几何体的三视图，得出该几何体是一侧面垂直于底面的三棱锥，画出直观图，根据数据求出体积．

解答 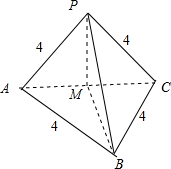解：根据几何体的三视图，得；
该几何体是侧面PAC⊥底面ABC的三棱锥，如图所示；
过点P作PM⊥AC，交AC与点M，连接BM，
则PM⊥平面ABC，且PM=2$\sqrt{2}$，
∴BM⊥AC，且BM=2$\sqrt{2}$，
∴AC=2AM=2$\sqrt{16-8}$=4$\sqrt{2}$，
∴三棱锥的体积为
V_{三棱锥P-ABC}=$\frac{1}{3}×\frac{1}{2}×4\sqrt{2}×2\sqrt{2}×2\sqrt{2}$=$\frac{16\sqrt{2}}{3}$．
故答案为$\frac{16\sqrt{2}}{3}$．

点评 本题考查了利用几何体的三视图求体积的应用问题，是基础题目．