练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．（x+y）（x2+x+y）5的展开式中，x5y2的系数为（　　）
    A．30B．40C．50D．60

    分析 求（x+y）（x2+x+y）5的展开式中x5y2的系数，只要分析此项的构成以及来源，利用二项式定理解答．

    解答 解：（x+y）（x2+x+y）5的展开式中x5y2，可以是x•x4y2，也可以是y•x5y，
    而（x2+x+y）5的表示5个因式（x2+x+y）的乘积，
    若其中2个因式取y，其余的3个因式中有一个取x2、2个取x，可得含x4y2的项，故x4y2的系数为${C}_{5}^{2}$•${C}_{3}^{1}$=30．
    若其中1个因式取y，其余的4个因式中有1个取x2，其余的3个都取x，可得含x5y的项，故x5y的系数为${C}_{5}^{1}$•${C}_{4}^{1}$=20．
    故x5y2的系数为50，
    故选：C．

    点评 本题考查了二项式定理的运用，关键是明确（x+y）（x2+x+y）5的展开式中x5y2的构成是两个二项式的哪些项相乘得到，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．奇函数f（x）在[0，+∞）单调递增，则f（-2）≤f（x2-3x）≤0整数解有（　　）个．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

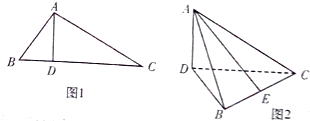    9．如图1，在Rt△ABC中，∠ABC=60°，∠BAC=90°，AD是BC上的高，沿AD将△ABC折成600的二面角B-AD-C，如图2．
    （1）证明：平面ABD⊥平面BCD．
    （2）设E为BC的中点，BD=2，求异面直线AE与BD所成的角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=|2x-1|+|x+1|．
    （Ⅰ）求不等式f（x）≥2的解集；
    （Ⅱ）若关于x的不等式f（x）＜a的解集为∅，求参数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：
    ①若m⊥α，m⊥β，则α∥β；
    ②若m?α，n?β，m∥n，则α∥β；
    ③若α⊥γ，β⊥γ，则α∥β；
    ④若m、n是异面直线，m?α，m∥β，n?β，n∥α，则α∥β
    其中真命题是（　　）
    A．①和②B．①和③C．①和④D．③和④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．一个几何体的三视图如图所示，其中左视图为直角三角形，则该几何体的体积为$\frac{16\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．利用基本不等式求最值，下列各式运用正确的是（　　）
    A．$y=x+\frac{4}{x}≥2\sqrt{x•\frac{4}{x}}=4$
    B．$y=sinx+\frac{4}{sinx}≥2\sqrt{sinx•\frac{4}{sinx}}=4\;（x为锐角）$
    C．$y=lgx+4{log_x}10≥2\sqrt{lgx•4{{log}_x}10}=4$
    D．$y={3^x}+\frac{4}{3^x}≥2\sqrt{{3^x}•\frac{4}{3^x}}=4$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．长为2$\sqrt{2}$线段EF的两上端点E、F分别在坐标轴x轴、y轴上滑动，设线段中点为M，线段EF在滑动过程中，点M形成轨迹为C．
    （1）求C的方程；
    （2）过点P（0，1）直线l与轨迹C交于A、B两点．
    ①写出$\frac{{|{AP}|}}{{|{PB}|}}$的取值范围，可简要说明理由；
    ②坐标平面内是否存在异于点P的定点Q，当l转动时，总有$\frac{{|{QA}|}}{{|{QB}|}}=\frac{{|{PA}|}}{{|{PB}|}}$恒成立？若存在，请求出Q点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．现有下列命题：
    ①?x∈R，不等式x2+2x＞4x-3均成立；
    ②若log2x+logx2≥2，则x＞1；
    ③“若a＞b＞0且c＜0，则$\frac{c}{a}$＞$\frac{c}{b}$”的逆否命题是真命题；
    ④若命题p：?x∈R，x2+1≥1，命题q：?x0∈R，x02-x0-1≤0，则命题p∧￢q是真命题．
    则其中真命题为（　　）
    A．①②③B．①②④C．①③④D．②③④

    查看答案和解析>>

    同步练习册答案