
分析 (1)利用已知条件,转化为|OM|的距离,求解轨迹方程即可.
(2)①设直线l与轨迹C交于A、B两点,当直线的斜率不存在时,|AP|的最小值为:$\sqrt{2}-$1,最大值为:$\sqrt{2}+1$,|PB|的最小值为:$\sqrt{2}-$1,最大值为:$\sqrt{2}+1$,即可求出范围,
②分直线l的斜率不存在、存在两种情况,利用韦达定理及直线斜率计算方法,对任意直线l,均总有$\frac{{|{QA}|}}{{|{QB}|}}=\frac{{|{PA}|}}{{|{PB}|}}$恒成立,求出m的值.
解答 解:(1)长为2$\sqrt{2}$线段EF的两上端点E、F分别在坐标轴x轴、y轴上滑动,
设线段中点为M(x,y),可得|OM|=$\sqrt{2}$.
线段EF在滑动过程中,点M形成轨迹为C:x2+y2=2;
(2)①设直线l与轨迹C交于A、B两点,
当直线的斜率不存在时,|AP|的最小值为:$\sqrt{2}-$1,最大值为:$\sqrt{2}+1$,
|PB|的最小值为:$\sqrt{2}-$1,最大值为:$\sqrt{2}+1$,
可知$\frac{{|{AP}|}}{{|{PB}|}}$∈[$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,$\frac{1+\sqrt{2}}{\sqrt{2}-1}$],即:$\frac{{|{AP}|}}{{|{PB}|}}$∈[3-2$\sqrt{2}$,3+2$\sqrt{2}$].
②当直线的斜率存在时设为k,过点P(0,1)直线l:y=kx+1,
A、B的坐标分别为A(x1,y1)、B(x2,y2),
由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}+{y}^{2}=2}\end{array}\right.$
消去y并整理得:(1+k2)x2+2kx-1=0,
∵△=(4k)2+4(1+2k2)>0,
∴x1+x2=$\frac{-2k}{1+{k}^{2}}$,x1x2=$\frac{-1}{1+{k}^{2}}$,
由|QA|•|PB|=|QB|•|PA|可得$\frac{{|{QA}|}}{{|{QB}|}}=\frac{{|{PA}|}}{{|{PB}|}}$,
知QP为∠AQP的角平分线,
由对称性易知,点Q必在y轴上,设Q(0,m),
于是有KQA+KQB=0,
∴$\frac{{y}_{1}-m}{{x}_{1}-0}$+$\frac{{y}_{2}-m}{{x}_{2}-m}$=0,
即(y1-m)x2+(y2-m)x1=0,且y1=kx1+1,y2=kx2+1,
∴(kx1+1-m)x2+(kx2+1-m)x1=0,
∴2kx1x2+(1-m)(x1+x2)=0,
∴2k•$\frac{-1}{1+{k}^{2}}$+$\frac{-2k}{1+{k}^{2}}$(1-m)=0,
∴$\frac{2k}{1+{k}^{2}}$[-1-(1-m)]=0,对任意k∈R恒成立,
则-1-(1-m)=0,
解得m=2,
特别的,当直线l的斜率不存在时,此时A(0,$\sqrt{2}$),B(0,-$\sqrt{2}$),Q(0.2),P(0,1)
$\frac{|QA|}{|QB|}$=$\frac{2-\sqrt{2}}{2+\sqrt{2}}$=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,$\frac{|PA|}{|PB|}$=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,
综上,平面上存在定点Q(0,2)时,当l转动时,总有$\frac{{|{QA}|}}{{|{QB}|}}=\frac{{|{PA}|}}{{|{PB}|}}$恒成立
点评 本题考查圆的标准方程与几何性质、直线方程,直线与椭圆的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化、特殊与一般、分类与整合等数学思想,属于难题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {1,2} | C. | {1} | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
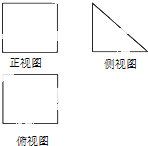
| A. | 4 | B. | 8 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com