
分析 由题意画出图形,设P的坐标为(x,y),由已知求出向量$\overrightarrow{AB}$,$\overrightarrow{AC}$的坐标,进而可得cos∠BAC值,求出sin∠BAC,可得区域D的面积S=$\sqrt{10}$(a-1)×$\sqrt{10}$(b-1)×sin∠BAC,然后利用基本不等式求得a+4b的最小值.
解答 解:如图所示,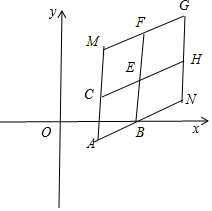
延长AB到点N,延长AC到点M,使得|AN|=a|AB|,|AM|=b|AC|,作CH∥AN,BF∥AM,NG∥AM,MG∥AN,则四边形ABEC,ANGM,EHGF均为平行四边形.由题意可知:点P(x,y)组成的区域D为图中的四边形EFGH及其内部.
∵点A(1,-1),B(4,0),C(2,2),
∴$\overrightarrow{AB}$=(3,1),$\overrightarrow{AC}$=(1,3),
则cos∠BAC=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}|•|\overrightarrow{AC}|}$=$\frac{3+3}{\sqrt{10}×\sqrt{10}}$=$\frac{3}{5}$,
∴sin∠BAC=$\frac{4}{5}$,
若平面区域D由所有满足$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$(1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.
则区域D的面积S=$\sqrt{10}$(a-1)×$\sqrt{10}$(b-1)×sin∠BAC=8[ab-(a+b)+1]=8,
∴(a-1)(b-1)=1,即$\frac{1}{a}+\frac{1}{b}=1$.
∴a+4b=(a+4b)$(\frac{1}{a}+\frac{1}{b})$=5+$\frac{a}{b}+\frac{4b}{a}$≥5$+2\sqrt{\frac{a}{b}•\frac{4b}{a}}$=9,当且仅当a=2b=3时取等号.
∴a+4b的最小值为9.
故答案为:9.
点评 本题考查的知识点是平面向量的基本定理,其中求出区域D的面积S=$\sqrt{10}$(a-1)×$\sqrt{10}$(b-1)×sin∠BAC是解答的关键,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7\sqrt{2}}{2}$ | B. | $\sqrt{29}$ | C. | 5 | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
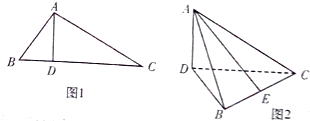 如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD将△ABC折成600的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD将△ABC折成600的二面角B-AD-C,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com