
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
, ![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() ,
,![]() .
.

(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() //平面
//平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在第(2)问条件下,设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求当
,求当![]() 取最大值时点
取最大值时点![]() 的位置.
的位置.
【答案】(1)见解析;(2)![]() ;(3)即点N在线段CD上且
;(3)即点N在线段CD上且![]()
【解析】
(1)取线段SC的中点E,连接ME,ED.可证![]() 是平行四边形,从而有
是平行四边形,从而有![]() ,则可得线面平行;
,则可得线面平行;
(2)以点A为坐标原点,建立分别以AD、AB、AS所在的直线为x轴、y轴、z轴建立空间直角坐标系,求出两平面![]() 与平面
与平面![]() 的法向量,由法向量夹角的余弦值可得二面角的余弦值;
的法向量,由法向量夹角的余弦值可得二面角的余弦值;
(3)设![]() ,其中
,其中![]() ,求出
,求出![]() ,由MN与平面
,由MN与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 与平面
与平面![]() 的法向量夹角余弦值的绝对值可求得结论.
的法向量夹角余弦值的绝对值可求得结论.
(1)证明:取线段SC的中点E,连接ME,ED.

在![]() 中,ME为中位线,∴
中,ME为中位线,∴![]() 且
且![]() ,
,
∵![]() 且
且![]() ,∴
,∴![]() 且
且![]() ,
,
∴四边形AMED为平行四边形.
∴![]() .
.
∵![]() 平面SCD,
平面SCD,![]() 平面SCD,
平面SCD,
∴![]() 平面SCD.
平面SCD.
(2)解:如图所示以点A为坐标原点,建立分别以AD、AB、AS所在的直线为x轴、y轴、z轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
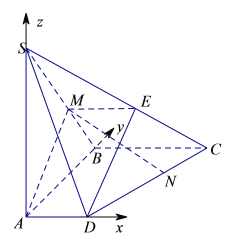
由条件得M为线段SB近B点的三等分点.
于是![]() ,即
,即![]() ,
,
设平面AMC的一个法向量为![]() ,则
,则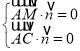 ,
,
将坐标代入并取![]() ,得
,得![]() .
.
另外易知平面SAB的一个法向量为![]()
![]() ,
,
所以平面AMC与平面SAB所成的锐二面角的余弦为![]()
![]() .
.
(3)设![]() ,其中
,其中![]() .
.
由于![]() ,所以
,所以![]()
![]() .
.
所以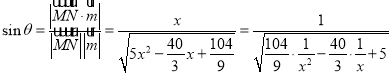 ,
,
可知当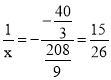 ,即
,即![]() 时分母有最小值,此时
时分母有最小值,此时![]() 有最大值,
有最大值,
此时,![]() ,即点N在线段CD上且
,即点N在线段CD上且![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱![]() 的侧棱垂直于底面,且底面是边长为2的正三角形,
的侧棱垂直于底面,且底面是边长为2的正三角形,![]() ,点D,E,F分别是所在棱的中点.
,点D,E,F分别是所在棱的中点.

(1)在线段![]() 上找一点
上找一点![]() 使得平面
使得平面![]() ∥平面
∥平面![]() ,给出
,给出![]() 点的位置并证明你的结论;
点的位置并证明你的结论;
(2)在(1)的条件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时期著名的数学家刘徽对推导特殊数列的求和公式很感兴趣,创造并发展了许多算法,展现了聪明才智.他在《九章算术》“盈不足”章的第19题的注文中给出了一个特殊数列的求和公式.这个题的大意是:一匹良马和一匹驽马由长安出发至齐地,长安与齐地相距3000里(1里=500米),良马第一天走193里,以后每天比前一天多走13里.驽马第一天走97里,以后每天比前一天少走半里.良马先到齐地后,马上返回长安迎驽马,问两匹马在第几天相遇( )
A. 14天B. 15天C. 16天D. 17天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 为
为![]() 个正数
个正数![]() 、
、![]() 、
、![]() 、
、![]() 的“均倒数”.已知正项数列
的“均倒数”.已知正项数列![]() 的前
的前![]() 项的“均倒数”为
项的“均倒数”为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列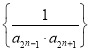 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对一切
对一切![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,问:是否存在正整数
,问:是否存在正整数![]() 使得
使得![]() 对一切
对一切![]() 恒成立,如存在,求出
恒成立,如存在,求出![]() 值,否则说明理由.
值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大气污染是我国目前最突出的环境问题之一,其中工厂废气是大气污染的重大污染源之一。工厂废气未经净化处理排放至空气中,除了对空气质量造成严重破坏,还会对人体的健康造成重大威胁。长期生活在污染的空气中,生活质量及身体健康将急剧下降。某工厂因为污染问题需改进技术,2019年初购进一台环保新机器投入生产,机器的成本价为36万元,第![]() 年该机器包括维修费和机器护理费用在内,每年另需投人费用
年该机器包括维修费和机器护理费用在内,每年另需投人费用![]() 万元,购进该机器后每年盈利20万元.
万元,购进该机器后每年盈利20万元.
(1)问该机器投入生产第几年,工厂开始盈利(即总收入大于所有投人的费用)?
(2)由于机器使用年限越大维修等费用越高,所以工厂决定当年平均利润最大时将该机器以5万元低价处理,问使用该机器几年后工厂年平均利润最大?此时工厂获得的总利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
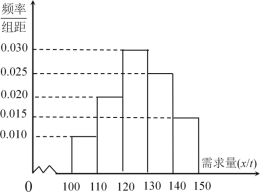
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上的一动点,点
上的一动点,点![]() ,点
,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴的交点分别为点
轴的正半轴的交点分别为点![]() ,
,![]() ,斜率为
,斜率为![]() 的动直线
的动直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,其中点
两点,其中点![]() 在第一象限,求四边形
在第一象限,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com