
 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△分析 (Ⅰ)取A1E的中点M,连接QM,MF,由三角形的中位线定理可得QM∥BE,且$QM=\frac{1}{2}BE$.再由已知可得PF∥BE,且PF=$\frac{1}{2}BE$,得到四边形PQMF为平行四边形.
有PQ∥FM.由线面平行的判定可得PQ∥平面A1EF;
(Ⅱ)在图1中取BE中点D,连接DF,结合已知可得△ADF是正三角形.进一步得到A1E⊥EF.再由平面A1EF⊥平面EFB,由面面垂直的性质可得A1E⊥平面EFB,从而得到A1E⊥EP;
(Ⅲ)作CN⊥BE于N,连接QN,则CN∥EF.由线面垂直的判定可得EF⊥平面A1BE.从而得到CN⊥平面A1BE,即∠CQN为CQ与平面A1BE所称的角.然后求解三角形得答案.
解答 (Ⅰ)证明:取A1E的中点M,连接QM,MF,
在△A1BE中,Q、M分别为A1B、A1E的中点,
∴QM∥BE,且$QM=\frac{1}{2}BE$.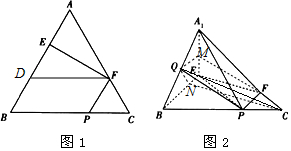
∵$\frac{CF}{FA}=\frac{CP}{PB}=\frac{1}{2}$,∴PF∥BE,且PF=$\frac{1}{2}BE$,
∴QM∥PF,且QM=PF,
∴四边形PQMF为平行四边形.
∴PQ∥FM.
又∵FM?平面A1EF,且PQ?平面A1EF,
∴PQ∥平面A1EF;
(Ⅱ)证明:在图1中取BE中点D,连接DF,
∵AE=CF=1,DE=1,∴AF=AD=2.
而∠A=60°,即△ADF是正三角形.
又∵AE=ED=1,∴EF⊥AD.
∴在图2中有A1E⊥EF.
∵平面A1EF⊥平面EFB,平面A1EF∩平面EFB=EF,
∴A1E⊥平面EFB,
由EP?平面EFB,得A1E⊥EP;
(Ⅲ)解:作CN⊥BE于N,连接QN,则CN∥EF.
∵EF⊥A1E,EF⊥BE,A1E∩BE=E,∴EF⊥平面A1BE.
因此,CN⊥平面A1BE,即QN是CQ在平面A1BE内的射影.
∴∠CQN为CQ与平面A1BE所称的角.
$CN=\frac{3\sqrt{3}}{2}$,$BQ=\frac{1}{2}{A}_{1}B=\frac{\sqrt{5}}{2}$,cos$∠{A}_{1}BE=\frac{2}{\sqrt{5}}$.
∴$Q{N}^{2}=B{Q}^{2}+B{N}^{2}-2BQ•BN•cos∠{A}_{1}BE=\frac{1}{2}$.
于是QN=$\frac{\sqrt{2}}{2}$.
∴tan∠CQN=$\frac{CN}{QN}=\frac{\frac{3\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}=\frac{3\sqrt{6}}{2}$.
即CQ与平面A1BE所成角的正切值为$\frac{3\sqrt{6}}{2}$.
点评 本题考查直线与平面平行、直线与平面垂直的判定,考查空间想象能力和思维能力,考查线面角的求法,正确找出CQ与平面A1BE所成角是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
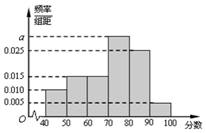 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com