
分析 (1)本题要求把小球全部放入盒子,1号小球可放入任意一个盒子内,有3种放法.余下的2、3、4,5,6号小球也各有3种放法,根据分步计数原理得到结果.
(2)分成三类:(2,2,2);(4,1,1);(1,2,3).先分组再排列,根据分类计数原理可得
解答 解:(1)乘法原理:63=216种不同的放法.
(2)分成三类:(2,2,2);(4,1,1);(1,2,3).先分组再排列.
第一类:$\frac{C_6^2•C_4^2•C_2^2}{A_3^3}•A_3^3=90$;
第二类:$C_6^4•\frac{C_2^1•C_1^1}{A_2^2}•A_3^3=90$;
第三类:$C_6^1•C_5^2•C_3^3•A_3^3=360$,
根据分类计数原理共有90+90+360=540种.
点评 本题考查排列、组合的运用,是常见的题型,要注意题意的要求,如本题中的小球、盒子是否相同.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
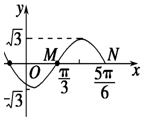 如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分.
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com