
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() 为R上的偶函数,且关于x的不等式
为R上的偶函数,且关于x的不等式![]() 在
在![]() 上恒成立,求实数k的取值范围.
上恒成立,求实数k的取值范围.
【答案】(1)![]() ,偶函数;
,偶函数;![]() ,奇函数;
,奇函数;![]() ,非奇非偶函数,理由见解析;(2)
,非奇非偶函数,理由见解析;(2)![]() .
.
【解析】
(1)根据函数奇偶性的定义即可判断函数f(x)的奇偶性;
(2)由题意可得![]() 在(﹣∞,0)上恒成立,求出右边函数的取值范围,可得k的不等式,解不等式即可得到所求范围.
在(﹣∞,0)上恒成立,求出右边函数的取值范围,可得k的不等式,解不等式即可得到所求范围.
(1)f(﹣x)=2﹣x+m2x,
若f(x)是偶函数,则f(﹣x)=f(x),即2﹣x+m2x=2x+m2﹣x,
所以(m﹣1)(2x﹣2﹣x)=0对任意实数x成立,所以m=1;
若f(x)是奇函数,则f(﹣x)=﹣f(x),即2﹣x+m2x=﹣2x﹣m2﹣x,
所以(m+1)(2x+2﹣x)=0对任意实数x成立,所以m=﹣1.
综上,当m=1时,f(x)是偶函数;当m=﹣1时,f(x)是奇函数;当m≠±1时,f(x)既不是奇函数也不是偶函数.
(2)f(x)![]() 0,3k2+1>0,
0,3k2+1>0,
且2kf(x)>3k2+1在(﹣∞,0)上恒成立,
故原不等式等价于![]() 在(﹣∞,0)上恒成立,
在(﹣∞,0)上恒成立,
又x∈(﹣∞,0),所以f(x)∈(2,+∞),
所以![]() ,
,
从而![]() ,即有3k2﹣4k+1≤0,
,即有3k2﹣4k+1≤0,
因此,![]() .
.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】某环境保护部门对某处的环境状况用“污染指数”来监测,据测定,该处的“污染指数”与附近污染源的强度和距离之比成正比,比例系数为常数![]()
![]() ,现已知相距
,现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为1和
两家化工厂(污染源)的污染强度分别为1和![]()
![]() ,它们连线段上任意一点
,它们连线段上任意一点![]() 处的污染指数
处的污染指数![]() 等于两化工厂对该处的污染指数之和,设
等于两化工厂对该处的污染指数之和,设![]() ;
;
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() 时,
时,![]() 处的“污染指数”最小,试求
处的“污染指数”最小,试求![]() 化工厂的污染强度
化工厂的污染强度![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆黄金周影市火爆依旧,《我和我的祖国》、《中国机长》、《攀登者》票房不断刷新,为了解我校高三2300名学生的观影情况,随机调查了100名在校学生,其中看过《我和我的祖国》或《中国机长》的学生共有80位,看过《中国机长》的学生共有60位,看过《中国机长》且看过《我和我的祖国》的学生共有50位,则该校高三年级看过《我和我的祖国》的学生人数的估计值为( )
A.1150B.1380C.1610D.1860
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由![]() 个不同的数构成的数列
个不同的数构成的数列![]() 中,若
中,若![]() 时,
时,![]() (即后面的项
(即后面的项![]() 小于前面项
小于前面项![]() ),则称
),则称![]() 与
与![]() 构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为
构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为![]() ;同理,等比数列
;同理,等比数列![]() 的逆序数为
的逆序数为![]() .
.
(1)计算数列![]() 的逆序数;
的逆序数;
(2)计算数列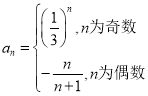 (
(![]() )的逆序数;
)的逆序数;
(3) 已知数列![]() 的逆序数为
的逆序数为![]() ,求
,求![]() 的逆序数.
的逆序数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为
的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为![]() ,且
,且![]() .
.
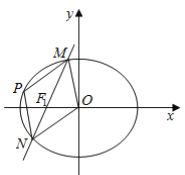
(1)求椭圆C的方程;
(2)过椭圆C的左焦点![]() 的直线
的直线![]() 交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线
交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
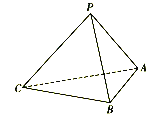
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:![]() 与直线
与直线![]() 交于A、B两点.
交于A、B两点.
(1)当![]() 取得最小值为
取得最小值为![]() 时,求
时,求![]() 的值.
的值.
(2)在(1)的条件下,过点![]() 作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且
作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且![]() 的平分线与
的平分线与![]() 轴平行,求证:直线MN的斜率为定值.
轴平行,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球教练对甲乙两位运动员在近五场比赛中的得分情况统计如下图所示,根据图表给出如下结论:(1)甲乙两人得分的平均数相等且甲的方差比乙的方差小;(2)甲乙两人得分的平均数相等且甲的方差比乙的方差大;(3)甲的成绩在不断提高,而乙的成绩无明显提高;(4)甲的成绩较稳定,乙的成续基本呈上升状态;结论正确的是( )
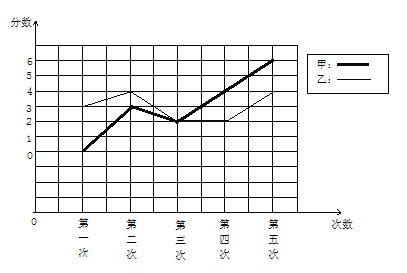
A.(1)(3)B.(1)(4)C.(2)(3)D.(2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com