
分析 (1)由题意列出方程组,求出a、b、c的关系,由两角和的正弦公式化简f(x),由a=2求出f(x),由x的范围和正弦函数的图象与性质,求出f(x)的值域;
(2)由x的范围和正弦函数的图象与性质,求出f(x)的最值,由条件和恒成立列出不等式,求出实数a的取值范围;
(3)由(1)和诱导公式化简f(x+$\frac{π}{4}$)f(x-$\frac{π}{4}$),代入不等式后结合条件化简,利用平方关系、换元法、分离常数法化简不等式,由条件和函数的单调性求出实数a的取值范围.
解答 解:(1)由题意得,f(x)的图象经过(0,1),($\frac{π}{2}$,1)两点,
∴$\left\{\begin{array}{l}{a+bcos0+csin0=1}\\{a+bcos\frac{π}{2}+csin\frac{π}{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{c=b}\\{a=1-b}\end{array}\right.$,
则f(x)=bsinx+bcosx+1-b=$\sqrt{2}bsin(x+\frac{π}{4})+1-b$,
又a=2,则b=c=-1,∴f(x)=$-\sqrt{2}sin(x+\frac{π}{4})+2$,
由x∈[0,$\frac{π}{2}$]得,$x+\frac{π}{4}∈[\frac{π}{4},\frac{3π}{4}]$,则$\frac{\sqrt{2}}{2}≤sin(x+\frac{π}{4})≤1$,
∴f(x)的值域是$[-\sqrt{2}+2,1]$;
(2)由(1)得,f(x)=$\sqrt{2}bsin(x+\frac{π}{4})+1-b$=$\sqrt{2}(1-a)sin(x+\frac{π}{4})+a$,
由x∈[0,$\frac{π}{2}$]得,$x+\frac{π}{4}∈[\frac{π}{4},\frac{3π}{4}]$,则$\frac{\sqrt{2}}{2}≤sin(x+\frac{π}{4})≤1$,
当$sin(x+\frac{π}{4})=1$ 时,f(x)=$\sqrt{2}(1-a)+a$=$\sqrt{2}+(1-\sqrt{2})a$,
当$sin(x+\frac{π}{4})=\frac{\sqrt{2}}{2}$时,f(x)=$\sqrt{2}(1-a)×\frac{\sqrt{2}}{2}+a$=1,
∵不等式|f(x)|≤2,在[0,$\frac{π}{2}$]上恒成立,
∴|$\sqrt{2}+(1-\sqrt{2})a$|≤2,解得$-\sqrt{2}≤a≤\sqrt{2}(3+2\sqrt{2})$,
即$-\sqrt{2}≤a≤4+3\sqrt{2}$,
∴实数a的取值范围是$[-\sqrt{2},4+3\sqrt{2}]$;
(3)由(1)得,f(x)=$\sqrt{2}(1-a)sin(x+\frac{π}{4})+a$,
∴f(x+$\frac{π}{4}$)f(x-$\frac{π}{4}$)=[$\sqrt{2}(1-a)sin(x+\frac{π}{2})+a$][$\sqrt{2}(1-a)sinx+a$]
=[$\sqrt{2}(1-a)cosx+a$][$\sqrt{2}(1-a)sinx+a$]
=$2{(1-a)}^{2}sinxcosx+\sqrt{2}a(1-a)(cosx+sinx)+{a}^{2}$,
代入不等式f(x+$\frac{π}{4}$)f(x-$\frac{π}{4}$)+a2-4a+2≥0得,
$2{(1-a)}^{2}sinxcosx+\sqrt{2}a(1-a)(cosx+sinx)$+2(a2-2a+1)≥0,
又a>1,$2(a-1)sinxcosx-\sqrt{2}a(cosx+sinx)+2(a-1)≥0$,①
设t=sinx+cosx,则2sinxcosx=t2-1,且t=$\sqrt{2}sin(x+\frac{π}{4})$,
由x∈[0,$\frac{π}{2}$]得,$x+\frac{π}{4}∈[\frac{π}{4},\frac{3π}{4}]$,则$\frac{\sqrt{2}}{2}≤sin(x+\frac{π}{4})≤1$,
∴t∈$[1,\sqrt{2}]$,代入①整理得,
(a-1)(t2-1)-$\sqrt{2}$at+2(a-1)≥0,则(a-1)t2-$\sqrt{2}$at+a-1≥0,
∵${t}^{2}-\sqrt{2}t+1>0$,∴$a≥\frac{{t}^{2}+1}{{t}^{2}-\sqrt{2}t+1}$=$\frac{{t}^{2}-\sqrt{2}t+1+\sqrt{2}t}{{t}^{2}-\sqrt{2}t+1}$=1+$\frac{\sqrt{2}t}{{t}^{2}-\sqrt{2}t+1}$,
设y=1+$\frac{\sqrt{2}t}{{t}^{2}-\sqrt{2}t+1}$=1+$\frac{\sqrt{2}}{t+\frac{1}{t}-\sqrt{2}}$,
∵函数y=$t+\frac{1}{t}$在$[1,\sqrt{2}]$上递增,∴函数y=1+$\frac{\sqrt{2}}{t+\frac{1}{t}-\sqrt{2}}$在$[1,\sqrt{2}]$上递减,
则此函数的最小值是1+$\frac{\sqrt{2}}{\sqrt{2}+\frac{1}{\sqrt{2}}-\sqrt{2}}$=3,
∵当a>1时,在[0,$\frac{π}{2}$]上存在x使不等式f(x+$\frac{π}{4}$)f(x-$\frac{π}{4}$)+a2-4a+2≥0成立,
∴实数a的取值范围是[3,+∞].
点评 本题考查正弦函数的图象与性质,三角恒等变换中的公式,函数的单调性,以及恒成立与存在性问题的转化,考查转化思想,换元法、分离常数法,化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
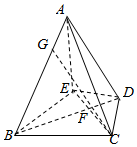 如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE,△BCE为正三角形,BD和CE的交点F,恰好平分CE,AE=BE=2,∠CDE=120°,AC=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE,△BCE为正三角形,BD和CE的交点F,恰好平分CE,AE=BE=2,∠CDE=120°,AC=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,以△ABC的BC边为直径的半圆交AB于点D,交AC于点E,EF⊥BC于F,BF:FC=5:1,AB=8,AE=2,则AD长为( )
如图,以△ABC的BC边为直径的半圆交AB于点D,交AC于点E,EF⊥BC于F,BF:FC=5:1,AB=8,AE=2,则AD长为( )| A. | $\frac{{1+\sqrt{21}}}{2}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1+\sqrt{2}}}{2}$ | D. | $\frac{43}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
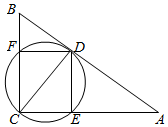 如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.
如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4032 | B. | 4036 | C. | 2016 | D. | 2018 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com