
已知函数f(x)=ln x+mx2(m∈R).
(1)求函数f(x)的单调区间;
(2)若A,B是函数f(x)图像上不同的两点,且直线AB的斜率恒大于1,求实数m的取值范围.
解:(1)f(x)的定义域为(0,+∞),
f′(x)=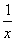 +2mx=
+2mx=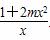 .
.
当m≥0时,f′(x)>0,f(x)在(0,+∞)上单调递增.
当m<0时,由f′(x)=0得x=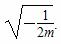 .
.
当x∈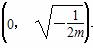 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在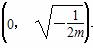 上单调递增;
上单调递增;
当x∈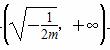 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在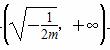 上单调递减.
上单调递减.
综上所述,当m≥0时,f(x)在(0,+∞)上单调递增;
当m<0时,f(x)在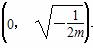 上单调递增,在
上单调递增,在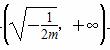 上单调递减.
上单调递减.
(2)依题意,设A(a,f(a)),B(b,f(b)),不妨设a>b>0,
则kAB=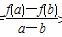 >1恒成立,
>1恒成立,
即f(a)-f(b)>a-b恒成立,
即f(a)-a>f(b)-b恒成立,
令g(x)=f(x)-x=ln x+mx2-x,
则g(x)在(0,+∞)上为增函数,
所以g′(x)=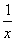 +2mx-1=
+2mx-1=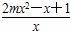 ≥0对x∈(0,+∞)恒成立,
≥0对x∈(0,+∞)恒成立,
所以2mx2-x+1≥0对x∈(0,+∞)恒成立,
即2m≥- +
+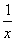 =-
=-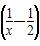 2+
2+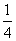 对x∈(0,+∞)恒成立,因此m≥
对x∈(0,+∞)恒成立,因此m≥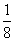 .
.
故实数m的取值范围为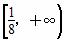 .
.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
函数f(x)=ax-1(a>0,a≠1)的图像恒过点A,下列函数中图像不经过点A的是( )
A.y=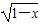 B.y=|x-2|
B.y=|x-2|
C.y=2x-1 D.y=log2(2x)
查看答案和解析>>
科目:高中数学 来源: 题型:
一高为H,满缸水量为V的鱼缸截面如图所示,其底部破了一个小洞 ,满缸水从洞中流出.若鱼缸水深为h时的水的体积为v,则函数v=f(h)的大致图像可能是图中的________.
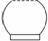
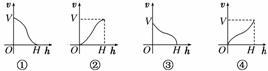
查看答案和解析>>
科目:高中数学 来源: 题型:
已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=ln x-ax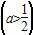 ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
A.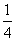 B.
B.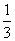
C. D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com