
已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心O在AB上,PO⊥平面ABC,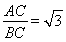 ,则三棱锥与球的体积之比为________.
,则三棱锥与球的体积之比为________.
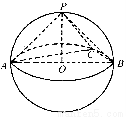
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:选择题
已知集合S={1,2},集合T={a},∅表示空集,如果S∪T=S,那么a的值是( )
A.∅ B.1
C.2 D.1或2
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )
A.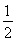 B.
B.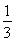 C.
C.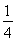 D.
D.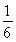
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知抛物线y2=2px(p>0)与双曲线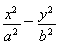 =1(a>0,b>0)的一条渐近线交于一点M(1,m),点M到抛物线焦点的距离为3,则双曲线的离心率等于( )
=1(a>0,b>0)的一条渐近线交于一点M(1,m),点M到抛物线焦点的距离为3,则双曲线的离心率等于( )
A.3 B.4 C.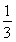 D.
D.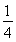
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.
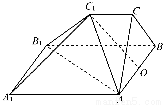
(1)若O是AB的中点,求证:OC1⊥A1B1;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在,确定点D的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
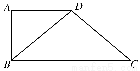
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为( )
A.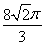 B.
B.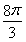 C.
C.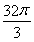 D.8π
D.8π
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
设z=x+y,其中实数x,y满足 若z的最大值为6,则z的最小值为( )
若z的最大值为6,则z的最小值为( )
A.-3 B.-2
C.-1 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com