
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0).
(1)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(2)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
【答案】
(1)
解:根据求导法则有 ![]() ,
,
故F(x)=xf'(x)=x﹣2lnx+2a,x>0,
于是 ![]() ,
,
∴知F(x)在(0,2)内是减函数,在(2,+∞)内是增函数,
所以,在x=2处取得极小值F(2)=2﹣2ln2+2a.
(2)
证明:由a≥0知,F(x)的极小值F(2)=2﹣2ln2+2a>0.
于是知,对一切x∈(0,+∞),恒有F(x)=xf'(x)>0.
从而当x>0时,恒有f'(x)>0,故f(x)在(0,+∞)内单调增加.
所以当x>1时,f(x)>f(1)=0,即x﹣1﹣ln2x+2alnx>0.
故当x>1时,恒有x>ln2x﹣2alnx+1.
【解析】(1)先根据求导法求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间及极值即可.(2)欲证x>ln2x﹣2a ln x+1,即证x﹣1﹣ln2x+2alnx>0,也就是要证f(x)>f(1),根据第一问的单调性即可证得.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某体育场要建造一个长方形游泳池,其容积为4800m3 , 深为3m,如果建造池壁的单价为a且建造池底的单价是建造池壁的1.5倍,怎样设计水池的长和宽,才能使总造价最底?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点
.不过原点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,且线段
两点,且线段![]() 被直线
被直线![]() 平分.
平分.
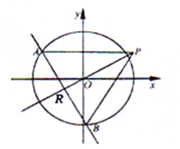
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的面积取最大值时直线
的面积取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
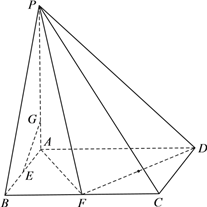
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA![]() 面ABCD,且AB=2,AD=4,
面ABCD,且AB=2,AD=4,
AP=4,F是线段BC的中点.
⑴ 求证:面PAF![]() 面PDF;
面PDF;
⑵ 若E是线段AB的中点,在线段AP上是否存在一点G,使得EG![]() 面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>1,f(x)=x2﹣ax , 当x∈(﹣1,1)时,均有f(x)< ![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.(1,2)
B.(1,3]
C.(1, ![]() )
)
D.(1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[0,1]上的函数f(x)满足:①f(0)=0;②f(x)+f(1﹣x)=1;③f( ![]() )=
)= ![]() f(x);④当0≤x1<x2≤1时,f(x1)≤f(x2).则f(
f(x);④当0≤x1<x2≤1时,f(x1)≤f(x2).则f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个图形F1 , F2 , 我们将图象F1上任意一点与图形F2上的任意一点间的距离中的最小值,叫作图形F1与F2图形的距离,若两个函数图象的距离小于1,则这两个函数互为“可及函数”,给出下列几对函数,其中互为“可及函数”的是 . (写出所有正确命题的编号) ①f(x)=cosx,g(x)=2;
②f(x)=ex . g(x)=x;
③f(x)=log2(x2﹣2x+5),g(x)=sin ![]() ﹣x;
﹣x;
④f(x)=x+ ![]() ,g(x)=lnx+2.
,g(x)=lnx+2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com