
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
【答案】
(1)解:从五张卡片中任取两张的所有可能情况有如下10种:红1红2,红1红3,红1蓝1,红1蓝2,红2红3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2.
其中两张卡片的颜色不同且标号之和小于4的有红1蓝1、红1蓝2、红2蓝1,共3种情况,
故所求的概率为 ![]() .
.
(2)解:加入一张标号为0的绿色卡片后,共有六张卡片,
从六张卡片中任取两张,有红1红2,红1红3,红1蓝1,红1蓝2,红2红3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2,红1绿0,红2绿0,红3绿0,蓝1绿0,蓝2绿0,共有15种情况,
其中颜色不同且标号之和小于4的有红1蓝1,红1蓝2,红2蓝1,红1绿0,红2绿0,红3绿0,蓝1绿0,蓝2绿0,共8种情况,
所以概率为 ![]() .
.
【解析】(1)由列举法可得从五张卡片中任取两张的所有情况,分析可得两张卡片的颜色不同且标号之和小于4的情况数目,由古典概型公式,计算可得答案;(2)加入一张标号为0的绿色卡片后,共有六张卡片,由列举法可得从中任取两张的所有情况,分析可得两张卡片的颜色不同且标号之和小于4的情况数目,由古典概型公式,计算可得答案.


科目:高中数学 来源: 题型:
【题目】某个体户计划经销A、B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A、B商品中所获得的收益分别为f(x)万元与g(x)万元、其中f(x)=a(x﹣1)+2(a>0);g(x)=6ln(x+b),(b>0)已知投资额为零时,收益为零.
(1)试求出a、b的值;
(2)如果该个体户准备投入5万元经营这两种商品,请你帮他制定一个资金投入方案,使他能获得最大收益,并求出其收入的最大值.(精确到0.1,参考数据:ln3≈1.10).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0).
(1)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(2)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
A.若mα,nα,l⊥m,l⊥n,则l⊥α
B.若mα,n⊥α,l⊥n,则l∥m
C.若l∥m,m⊥α,n⊥α,则l∥n
D.若l⊥m,l⊥n,则n∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点. 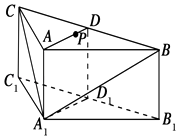
(1)在平面ABC内,试作出过点P与平面A1BC平行的直线l,并说明理由;
(2)证明:直线l⊥平面ADD1A1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆M:x2+y2﹣4x﹣2y+4=0
(1)若圆M的切线在x轴上的截距是y轴上的截距的2倍,求切线的方程;
(2)从圆外一点P(a,b),向该圆引切线PA,切点为A,且PA=PO,O为坐标原点,求证:以PM为直径的圆过异于M的定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,锐角△ABC中, ![]() =
= ![]() ,
, ![]() =
= ![]() ,点M为BC的中点. (Ⅰ)试用
,点M为BC的中点. (Ⅰ)试用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(Ⅱ)若| ![]() |=5,|
|=5,| ![]() |=3,sin∠BAC=
|=3,sin∠BAC= ![]() ,求中线AM的长.
,求中线AM的长.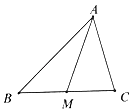
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|a≤x≤a+8},B={x|x<﹣1或x>5},
(1)当a=0时,求A∩B,A∪(CRB);
(2)若A∪B=B,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com