
分析 根据充要条件的定义,可判断①;求出常数项的值,可判断②;根据正态分布的对称性,可判断③.
解答 解:①“α=$\frac{π}{2}$”是“sinα=1”的充分不必要条件,故错误;
②($\frac{{x}^{3}}{2}$+$\frac{1}{x}$)4的展开式中的通项为:${C}_{4}^{r}(\frac{1}{2})^{4-r}{x}^{12-4r}$,
令12-4r=0,则r=3,由${C}_{4}^{3}{(\frac{1}{2})}^{4-3}$=2得:常数项为2,故正确;
③设随机变量ξ~N(0,1),若P(ξ≥1)=p,P(ξ≤-1)=p,P(-1<ξ<0)=$\frac{1}{2}$(1-2p)=$\frac{1}{2}$-p,故正确.
故答案为:②③
点评 本题以命题的真假判断与应用为载体,考查了充要条件,二项式定理,正态分布等知识点,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=18 B=$\frac{π}{6}$ A=$\frac{2π}{3}$ | B. | a=60 c=48 C=$\frac{2π}{3}$ | ||
| C. | a=3 b=6 A=$\frac{π}{6}$ | D. | a=14 b=15 A=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [${\frac{1}{2}$,2) | B. | [1,4] | C. | [${\frac{1}{4}$,4) | D. | [${\frac{1}{2}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
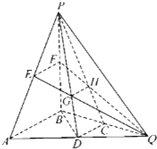 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com