Question

2．已知O为锐角三角形ABC的外心，∠B=30°，$\frac{cosA}{sinC}$$\overrightarrow{BA}$+$\frac{cosC}{sinA}$$\overrightarrow{BC}$=2m$\overrightarrow{OB}$，则实数m的值为$-\frac{1}{2}$．

Answer 1

分析 在等式$\frac{cosA}{sinC}\overrightarrow{BA}+\frac{cosC}{sinA}\overrightarrow{BC}=2m\overrightarrow{OB}$两边同时乘以向量$\overrightarrow{OB}$便可得到，$-\frac{cosA}{sinC}|\overrightarrow{BA}||\overrightarrow{OB}|cos∠ABO$$-\frac{cosC}{sinA}|\overrightarrow{BC}||\overrightarrow{OB}|cos∠CBO=2m{\overrightarrow{OB}}^{2}$．根据直角三角形边角关系有$\left|\overrightarrow{OB}\right|=\frac{\frac{1}{2}\left|\overrightarrow{BA}\right|}{cos∠ABO}=\frac{\frac{1}{2}\left|\overrightarrow{BC}\right|}{cos∠CBO}$，带入上式便得到$\frac{1}{2}•\frac{cosA}{sinC}•|\overrightarrow{BA}{|}^{2}+\frac{1}{2}•\frac{cosC}{sinA}•|\overrightarrow{BC}{|}^{2}=-2m|\overrightarrow{OB}{|}^{2}$，这样根据正弦定理便可得出cosAsinC+cosCsinA=-m，从而得到m=-sinB=$-\frac{1}{2}$．

解答 解：如图，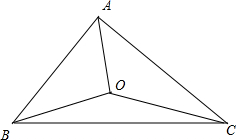

由$\frac{cosA}{sinC}\overrightarrow{BA}+\frac{cosC}{sinA}\overrightarrow{BC}=2m\overrightarrow{OB}$得$\frac{cosA}{sinC}\overrightarrow{BA}?\overrightarrow{OB}+\frac{cosC}{sinA}\overrightarrow{BC}?\overrightarrow{OB}=2m{\overrightarrow{OB}}^{2}$；
∴$\frac{cosA}{sinC}\left|\overrightarrow{BA}\right|?\left|\overrightarrow{OB}\right|cos（π-∠ABO）+\frac{cosC}{sinA}\left|\overrightarrow{BC}\right|?\left|\overrightarrow{OB}\right|cos（π-∠CBO）=2m{\overrightarrow{OB}}^{2}$；
而$\left|\overrightarrow{OB}\right|=\frac{\frac{1}{2}\left|\overrightarrow{BA}\right|}{cos∠ABO}=\frac{\frac{1}{2}\left|\overrightarrow{BC}\right|}{cos∠CBO}$；
∴$\frac{cosA}{sinC}?\frac{1}{2}{\left|\overrightarrow{BA}\right|}^{2}+\frac{cosC}{sinA}?\frac{1}{2}{\left|\overrightarrow{BC}\right|}^{2}=-2m{\left|\overrightarrow{OB}\right|}^{2}$；
∴$\frac{cosA}{sinC}?{c}^{2}+\frac{cosC}{sinA}?{a}^{2}=-m{（2R）}^{2}$（其中R为三角形ABC外接圆的半径）；
∴$\frac{cosA}{sinC}?{（sinC）}^{2}+\frac{cosC}{sinA}?{（sinA）}^{2}=-m$；
∴$cosAsinC+cosCsinA=-m，-m=sin（A+C）=sinB=\frac{1}{2}，m=-\frac{1}{2}$．
故答案为：$-\frac{1}{2}$．

点评 考查三角形外心的概念，向量数量积的计算公式，直角三角形边角的关系，以及正弦定理，两角和的正弦公式，三角函数的诱导公式．