
【题目】干支历法是上古文明的产物,又称节气历或中国阳历,是一部深奥的历法.它是用60组各不相同的天干地支标记年月日时的历法.具体的算法如下:先用年份的尾数查出天干,如2013年3为癸;再用2013年除以12余数为9,9为巳.那么2013年就是癸巳年了,
天干 | 甲 | 乙 | 丙 | 丁 | 戊 | 己 | 庚 | 辛 | 壬 | 癸 | ||
4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | |||
地支 | 子 | 丑 | 寅 | 卯 | 辰 | 巳 | 午 | 未 | 申 | 酉 | 戌 | 亥 |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 |
2020年高三应届毕业生李东是壬午年出生,李东的父亲比他大25岁.问李东的父亲是哪一年出生( )
A.甲子B.乙丑C.丁巳D.丙卯
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
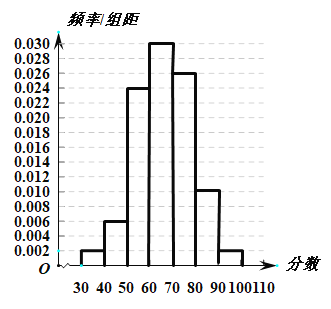
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
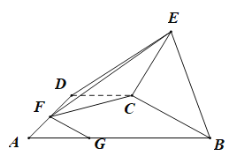
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(2)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
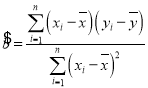 ,,
,,![]() 相关系数
相关系数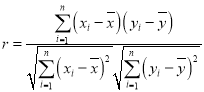
参考数据: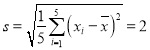 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,平面ABC是下底面.M是BB1上的点,AB=3,BC=4,AC=5,CC1=7,过三点A、M、C1作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据相关数据统计,2019年底全国已开通![]() 基站13万个,部分省市的政府工作报告将“推进
基站13万个,部分省市的政府工作报告将“推进![]() 通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
(1)如果从2月份起,以后的每个月比上一个月多建设2000个,那么,今年底全国共有基站多少万个.(精确到0.1万个)
(2)如果计划今年新建基站60万个,到2022年底全国至少需要800万个,并且,今后新建的数量每年比上一年以等比递增,问2021年和2022年至少各建多少万个オ能完成计划?(精确到1万个)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() 交椭圆于
交椭圆于![]() ,且
,且![]() ,
,![]() 的内切圆
的内切圆![]() 半径为1.
半径为1.
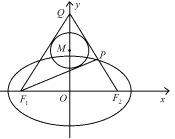
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 点为圆
点为圆![]() 上一点,求
上一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com