

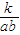 ,其中k>0为比例系数.依题意,即所求的a,b值使y值最小.
,其中k>0为比例系数.依题意,即所求的a,b值使y值最小.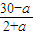 (0<a<30).①
(0<a<30).①
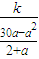 =
=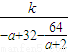 =
=
 =
=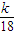 ,
,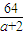 时取等号,y达到最小值.
时取等号,y达到最小值. ,
,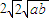 +ab≤30,
+ab≤30,

科目:高中数学 来源: 题型:
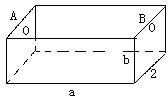 如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).
如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).查看答案和解析>>
科目:高中数学 来源: 题型:
如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从![]() 孔流入,经沉淀后从
孔流入,经沉淀后从![]() 孔流出,设箱体的长为
孔流出,设箱体的长为![]() 米,高为
米,高为![]() 米.已知流出的水中该杂质的质量分数与
米.已知流出的水中该杂质的质量分数与![]() ,
,![]() 的乘积
的乘积![]() 成反比,现有制箱材料60平方米,问当
成反比,现有制箱材料60平方米,问当![]() ,
,![]() 各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(
各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(![]() ,
,![]() 孔的面积忽略不计).
孔的面积忽略不计).

查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com