
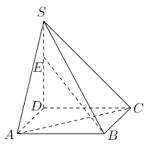
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点.
上任意一点.
(1)求证:![]() ;
;
(2)试确定点![]() 的位置,使
的位置,使![]() 与平面
与平面![]() 所成角的大小为30°.
所成角的大小为30°.
【答案】(1)证明见解析(2)当![]() 时,
时,![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]()
【解析】
(1)连结![]() ,通过证明
,通过证明![]() 平面
平面![]() ,即可得
,即可得![]() .另外可以利用空间向量证明线线垂直;
.另外可以利用空间向量证明线线垂直;
(2)由![]() ⊥平面
⊥平面![]() 可得
可得![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,在
,在![]() 中可求出
中可求出![]() 值,即可得到点
值,即可得到点![]() 的位置.另外还可以用空间向量法求线面角.
的位置.另外还可以用空间向量法求线面角.
(1)证明:连结![]() ,因为四边形
,因为四边形![]() 为正方形,
为正方形,
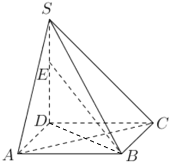
所以,![]() ,
,
又因为![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .由
.由
![]()
![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解法一:设![]() ,因为
,因为![]() ⊥平面
⊥平面![]() ,
,
所以![]() 与平面
与平面![]() 所成角为
所成角为![]()
在![]() 中,由
中,由![]()
![]()
![]()
![]() .
.
所以,当![]() 时,
时,![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
解法2:(1)以![]() 为坐标原点,建立空间直角坐标系.
为坐标原点,建立空间直角坐标系.
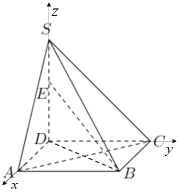
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]()
则![]() ,
,![]()
因为![]() ,
,
所以![]() ;
;
(2)取平面![]() 的一个法向量为
的一个法向量为![]()
因为![]() ,可知直线
,可知直线![]() 的一个方向向量为
的一个方向向量为![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由题意知
,由题意知![]()
![]() .
.![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
则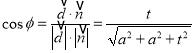 ,
,
因为![]() ,所以,
,所以,![]() ,
,
解得,![]() .
.
当![]() 时,
时,![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图.(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论错误的是( )
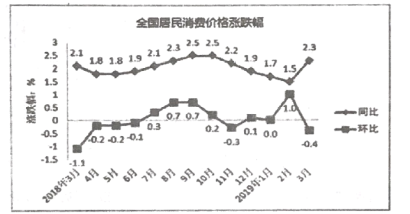
A.2018年3月至2019年3月全国居民消费价格同比均上涨
B.2018年3月至2019年3月全国居民消费价格环比有涨有跌
C.2019年3月全国居民消费价格同比涨幅最大
D.2019年3月全国居民消费价格环比变化最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为1的正方形ABCD沿x轴正向滚动,先以A为中心顺时针旋转,当B落在x轴时,又以B为中心顺时针旋转,如此下去,设顶点C滚动时的曲线方程为![]() ,则下列说法不正确的是
,则下列说法不正确的是![]()

A.![]() 恒成立B.
恒成立B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两座建筑物![]() ,
,![]() 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是![]() 和
和![]() ,从建筑物
,从建筑物![]() 的顶部
的顶部![]() 看建筑物
看建筑物![]() 的视角
的视角![]() .
.
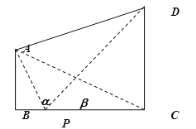
(1)求![]() 的长度;
的长度;
(2)在线段![]() 上取一点
上取一点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合),从点
不重合),从点![]() 看这两座建筑物的视角分别为
看这两座建筑物的视角分别为![]() ,
,![]() ,问点
,问点![]() 在何处时,
在何处时,![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是抛物线E:y2=4x上的动点,F是抛物线E的焦点.
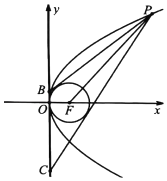
(1)求|PF|的最小值;
(2)点B,C在y轴上,直线PB,PC与圆(x﹣1)2+y2=1相切.当|PF|∈[4,6]时,求|BC|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0 (n∈N ),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设![]() ,数列{bn}的前n项和为Sn,当
,数列{bn}的前n项和为Sn,当![]() 最大时,求n的值.
最大时,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com