
【题目】已知函数![]()
(1)讨论f(x)的单调性;
(2)若f(x)有两个零点,求a的取值范围.
【答案】(1)见解析;(2) ![]()
【解析】
(1)先求导数,再讨论导函数零点,最后根据区间导函数符号确定单调性,
(2)结合函数单调性以及零点存在定理分类讨论零点个数,即得结果
解(1)![]()
(ⅰ)![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以f(x)在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
(ⅱ)![]() 时
时
若![]() ,则
,则![]() ,所以f(x)在
,所以f(x)在![]() 单调递增;
单调递增;
若![]() ,则
,则![]() ,故当
,故当![]() 时,
时,![]() ,
, ![]() ,
,![]() ;所以f(x)在
;所以f(x)在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
若![]() ,则
,则![]() ,故当
,故当![]() ,
,![]() ,
, ![]() ,
,![]() ;所以f(x)在
;所以f(x)在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
综上:![]() 时,f(x)在
时,f(x)在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
![]() 时,f(x)在
时,f(x)在![]() 单调递增;
单调递增;
![]() 时,f(x)在
时,f(x)在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
![]() 时,f(x)在
时,f(x)在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
(2)(ⅰ)当a>0,则由(1)知f(x)在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
又![]() ,
,![]() ,取b满足
,取b满足![]() ,且
,且![]() ,
,
则![]() ,所以f(x)有两个零点
,所以f(x)有两个零点
(ⅱ)当a=0,则![]() ,所以f(x)只有一个零点
,所以f(x)只有一个零点
(ⅲ)当a<0,若![]() ,则由(1)知,f(x)在
,则由(1)知,f(x)在![]() 单调递增.又当
单调递增.又当![]() 时,
时,![]() ,故f(x)不存在两个零点
,故f(x)不存在两个零点
![]() ,则由(1)知,f(x)在
,则由(1)知,f(x)在![]() 单调递减,在
单调递减,在![]() 单调递增,又当
单调递增,又当![]() ,f(x)<0,故f(x)不存在两个零点
,f(x)<0,故f(x)不存在两个零点
综上,a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
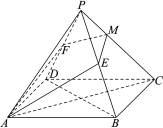
(1)求正四棱锥![]() 的全面积;
的全面积;
(2)若平面![]() 与棱
与棱![]() 交于点
交于点![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的大小(用反三角函数值表示).
所成锐二面角的大小(用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如题所示:扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条三条商业街道PQ、QR、RP,要求街道PQ与AB垂直,街道PR与AC垂直,直线PQ表示第三条街道。
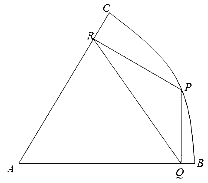
(1)如果P位于弧BC的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道PQ、PR、QR每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?(精确到1万元)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com