
【题目】如图三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() .
.

(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,
,![]() ,AB=BC,求二面角
,AB=BC,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
试题分析:(1)由四边形![]() 是菱形可以得到
是菱形可以得到![]() ,结合
,结合![]() 有
有![]() 平面
平面![]() ,因此
,因此![]() ,根据
,根据![]() 是
是![]() 的中点得到
的中点得到![]() .(2)由题设条件可证明
.(2)由题设条件可证明![]() ,从而
,从而![]() 两两相互垂直,设
两两相互垂直,设![]() 为单位长,则建立如图所示空间直角坐标系
为单位长,则建立如图所示空间直角坐标系![]() ,通过计算半平面的法向量的夹角来计算二面角的余弦值.
,通过计算半平面的法向量的夹角来计算二面角的余弦值.
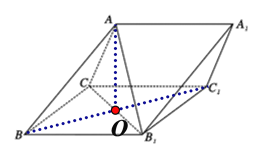
解析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,因为侧面
,因为侧面![]() 为菱形,所以
为菱形,所以![]() ,且
,且![]() 为
为![]() 及
及![]() 的中点,又
的中点,又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .由于
.由于![]() 平面
平面![]() ,故
,故![]() .又
.又![]() ,故
,故![]() .
.
(2)因为![]() ,且
,且![]() 为
为![]() 的中点,所以
的中点,所以![]() .又因为
.又因为![]() ,所以
,所以![]() ,故
,故![]() ,从而
,从而![]() 两两相互垂直,
两两相互垂直,![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长,建立如图所示空间直角坐标系
为单位长,建立如图所示空间直角坐标系![]() .
.
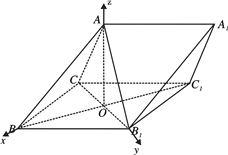
因为![]() ,所以
,所以![]() 为等边三角形,又
为等边三角形,又![]() ,则
,则![]() ,
,![]() .
.![]() ,
,![]() ,设
,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则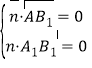 ,即
,即 ,所以可取
,所以可取![]() ,设
,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则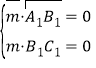 ,同理可取
,同理可取![]() ,
,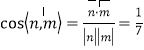 ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax,其中e为自然对数的底数,a为常数.
(1)若对函数f(x)存在极小值,且极小值为0,求a的值;
(2)若对任意x∈[0, ![]() ],不等式f(x)≥ex(1﹣sinx)恒成立,求a的取值范围.
],不等式f(x)≥ex(1﹣sinx)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,F是椭圆C的右焦点.过点F且斜率为k(k≠0)的直线l与椭圆C交于A,B两点,O是坐标原点.
,F是椭圆C的右焦点.过点F且斜率为k(k≠0)的直线l与椭圆C交于A,B两点,O是坐标原点.
(1)求n的值;
(2)若线段AB的垂直平分线在y轴的截距为 ![]() ,求k的值;
,求k的值;
(3)是否存在点P(t,0),使得PF为∠APB的平分线?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.
(求:S2= ![]() [
[ ![]() +
+ ![]() +…+
+…+ ![]() ],其中
],其中 ![]() 为数据x1 , x2 , …,xn的平均数)
为数据x1 , x2 , …,xn的平均数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com