
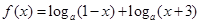 ,其中
,其中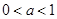 ,记函数
,记函数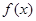 的定义域为D.
的定义域为D.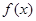 的定义域D;
的定义域D;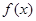 的最小值为
的最小值为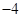 ,求
,求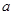 的值;
的值;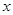 ,不等式
,不等式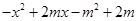 <
<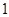 恒成立,求实数
恒成立,求实数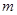 的取值范围.
的取值范围.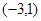
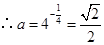
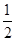 )∪[
)∪[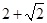 ,+∞)
,+∞)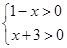 ,解得
,解得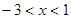
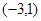 2分
2分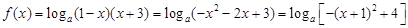
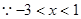
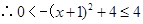
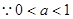 ,
,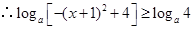 ,即
,即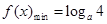 , 5分
, 5分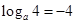 ,得
,得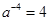 ,
,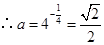 . 7分
. 7分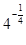 不化简为
不化简为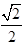 扣1分)
扣1分)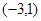 上恒成立,
上恒成立,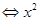 -2mx+m2-2m+1>0在x∈
-2mx+m2-2m+1>0在x∈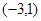 上恒成立, 8分
上恒成立, 8分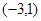 ,
,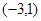 为增函数,
为增函数,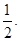 ∴-3<m<
∴-3<m<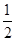 12分
12分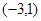 为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,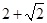 或m≤
或m≤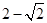 , ∴-3<m<
, ∴-3<m<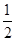 14分
14分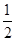 )∪[
)∪[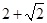 ,+∞) 16分
,+∞) 16分

 小学教材全测系列答案
小学教材全测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com