Question

已知双曲线

x2

16

-

y2

25

=1的左焦点为F₁，点P为双曲线右支上一点，且PF₁与圆x²+y²=16相切于点N，M为线段PF₁的中点，O为坐标原点，则|MN|-|MO|=

 

．

Answer 1

分析：根据双曲线方程算出a=4、b=5，可得c=

41

．连结ON、PF₂，根据圆的切线的性质与勾股定理算出|F₁N|=5，再在△PF₁F₂中利用中位线定理算出|MO|=

1

2

|PF₂|，利用双曲线的定义加以计算，即可得到|MN|-|MO|的值．

解答：解：∵双曲线

x2

16

-

y2

25

=1中，a=4且b=5，
∴c=

a2+b2

=

41

．
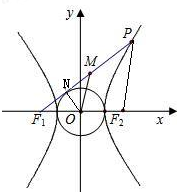
连结ON、PF₂，
∵PF₁与圆x²+y²=16相切于点N，∴ON⊥F₁P，
在Rt△ONF₁中，|F₁N|=

c2-a2

=5
∵△PF₁F₂中，M为线段F₁P的中点，O为坐标原点，∴|MO|=

1

2

|PF₂|，
由此可得：|MN|-|MO|=|MF₁|-|F₁N|-

1

2

|PF₂|=

1

2

（|PF₁|-|PF₂|）-5
∵点P在双曲线的右支上，可得|PF₁|-|PF₂|=2a=8，
∴|MN|-|MO|=

1

2

（|PF₁|-|PF₂|）-5=

1

2

×8-5=-1．
故答案为：-1

点评：本题主要考查双曲线的定义、三角形中位线、直线与圆相切与勾股定理等知识，属于中档题．解答的关键是熟悉双曲线的定义的应用，直线与圆的位置关系以及三角形中的有关结论．