
已知函数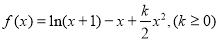 ,(提示:
,(提示: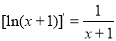 )
)
(1)当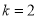 时,求曲线
时,求曲线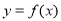 在点
在点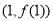 处的切线方程;
处的切线方程;
(2)求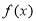 的单调区间.
的单调区间.
(1)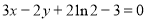 ;(2)①当
;(2)①当 时,
时,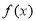 的单调递增区间是
的单调递增区间是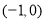 ,单调递减区间是
,单调递减区间是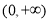 ;②当
;②当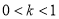 时,
时, 的单调递增区间是
的单调递增区间是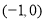 ,单调递减区间是
,单调递减区间是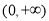 ;③当
;③当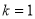 时,
时,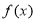 的单调递增区间是
的单调递增区间是 ;④当
;④当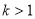 时,
时,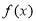 的单调递增区间是
的单调递增区间是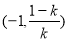 和
和 ,单调递减区间是
,单调递减区间是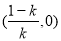 .
.
【解析】
试题分析:(1)当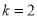 时,找到切点坐标和切线斜率,进而求得切线方程;(2)根据导函数的函数式。对
时,找到切点坐标和切线斜率,进而求得切线方程;(2)根据导函数的函数式。对 进行分类讨论,
进行分类讨论,
试题解析:因为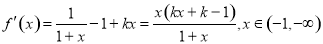
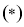
(1)当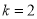 时,
时,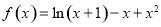 ,
,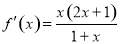 ,
,
所以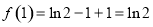 且
且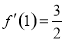 ,所以切点为
,所以切点为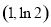 ,切线的斜率为
,切线的斜率为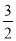 ,所求切线方程为:
,所求切线方程为: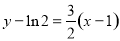 化简为:
化简为: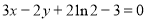 .
.
(2)根据 式进行分类讨论:按
式进行分类讨论:按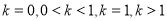 分别进行讨论,根据函数的导函数和原函数的单调性的关系分别找到单调区间.
分别进行讨论,根据函数的导函数和原函数的单调性的关系分别找到单调区间.
①当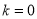 时,
时,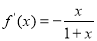
所以,在区间 上,
上,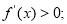 在区间
在区间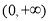 上,
上,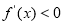
故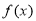 的单调递增区间是
的单调递增区间是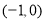 ,单调递减区间是
,单调递减区间是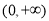 .
.
②当 时,由
时,由 得
得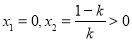 所以,在区间
所以,在区间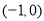 和
和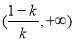 上,
上,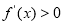 ,在区间
,在区间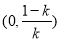 上
上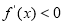
故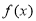 的单调递增区间是
的单调递增区间是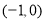 和
和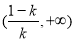 ,单调递减区间是
,单调递减区间是 .
.
③ 当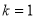 时,
时,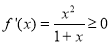 恒成立,故
恒成立,故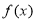 的单调递增区间是
的单调递增区间是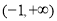 .
.
④ 当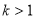 时,由
时,由 得
得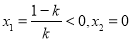
所以,在区间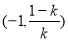 和
和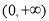 上,
上,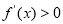 ,
,
在区间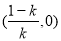 上
上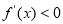
故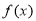 的单调递增区间是
的单调递增区间是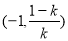 和
和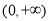 ,单调递减区间是
,单调递减区间是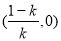 .
.
综上所述,①当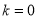 时,
时,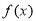 的单调递增区间是
的单调递增区间是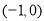 ,单调递减区间是
,单调递减区间是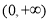 ;②当
;②当 时,
时,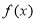 的单调递增区间是
的单调递增区间是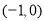 ,单调递减区间是
,单调递减区间是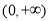 ;③当
;③当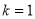 时,
时,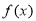 的单调递增区间是
的单调递增区间是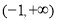 ;④当
;④当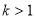 时,
时,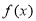 的单调递增区间是
的单调递增区间是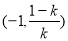 和
和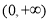 ,单调递减区间是
,单调递减区间是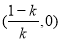 .
.
考点:1.利用导函数求切线方程;2.分类讨论思想.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2014-2015学年海市松江区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
已知函数 (
(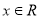 ,
,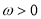 )的最小正周期为
)的最小正周期为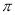 ,将
,将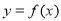 图像向左平移
图像向左平移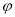 个单位长度
个单位长度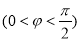 所得图像关于
所得图像关于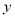 轴对称,则
轴对称,则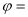 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
设第一象限内的点(x,y)满足约束条件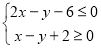 ,若目标函数z=ax+by(a>0,b>0)的最大值为40,则
,若目标函数z=ax+by(a>0,b>0)的最大值为40,则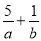 的最小值为( )
的最小值为( )
A、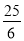 B、
B、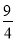 C、1 D、4
C、1 D、4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试文科数学试卷(解析版) 题型:选择题
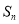 为等差数列
为等差数列 的前
的前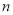 项和,已知
项和,已知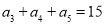 ,求
,求 ( )
( )
A、25 B、30 C、35 D、105
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北邢台一中高二12月月考文科数学试卷(解析版) 题型:选择题
下列有关命题的叙述, ①若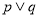 为真命题,则
为真命题,则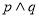 为真命题;②“
为真命题;②“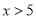 ”是“
”是“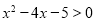 ”的充分不必要条件;③命题
”的充分不必要条件;③命题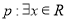 ,使得
,使得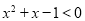 ,则
,则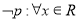 ,使得
,使得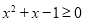 ;④命题“若
;④命题“若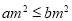 ,则
,则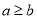 ”的否命题为真.其中错误的个数为( )
”的否命题为真.其中错误的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
圆心在y轴上且通过点(3,1)的圆与x轴相切,则该圆的方程是( )
A.x2+y2+10y=0 B.x2+y2-10y=0
C.x2+y2+10x=0 D.x2+y2-10x=0
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆Γ: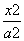 +
+ =1(a>b>0)的左、右焦点分别为F1、F2,焦距为2c,若直线y=
=1(a>b>0)的左、右焦点分别为F1、F2,焦距为2c,若直线y=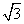 (x+c)与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com