
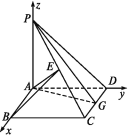
【题目】如图,ABCD是边长为a的正方形,PA⊥平面ABCD.

(1)若PA=AB,点E是PC的中点,求直线AE与平面PCD所成角的正弦值;
(2)若BE⊥PC且交点为E,BE=![]() a,G为CD的中点,线段AB上是否存在点F,使得EF∥平面PAG?若存在,求AF的长;若不存在,请说明理由.
a,G为CD的中点,线段AB上是否存在点F,使得EF∥平面PAG?若存在,求AF的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)以A为坐标原点建立坐标系,得出![]() 以及平面PCD的一个法向量,设直线AE与平面PCD所成角为
以及平面PCD的一个法向量,设直线AE与平面PCD所成角为![]() ,由sin
,由sin![]() =|cos<
=|cos<![]() ,m>|,即可求出直线AE与平面PCD所成角的正弦值。
,m>|,即可求出直线AE与平面PCD所成角的正弦值。
(2)设P(0,0,c)(c>0),![]() =λ
=λ![]() 由BE=
由BE=![]() a以及BE⊥PC可得λ=
a以及BE⊥PC可得λ=![]() ,c=a设AF=l,求出平面PAG的法向量为n,由
,c=a设AF=l,求出平面PAG的法向量为n,由![]() ·n=0即可得出答案。
·n=0即可得出答案。
(1)以A为原点,建立如图所示的坐标系,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,a),E![]() =(a,0,0),
=(a,0,0),![]() =(0,a,-a).
=(0,a,-a).
设平面PCD的法向量m=(x,y,z),则![]()
取m=(0,1,1),
则cos<![]() ,m>=
,m>=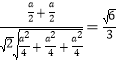 .
.
设直线AE与平面PCD所成角为![]() ,
,
则sin![]() =|cos<
=|cos<![]() ,m>|,所以直线AE与平面PCD所成角的正弦值为
,m>|,所以直线AE与平面PCD所成角的正弦值为![]() .
.
(2)G![]() ,设P(0,0,c)(c>0),
,设P(0,0,c)(c>0),
则![]() =(-a,-a,c).
=(-a,-a,c).
设![]() =λ
=λ![]() ,则E((1-λ)a,(1-λ)a,λc),
,则E((1-λ)a,(1-λ)a,λc),
∴![]() =(-λa,(1-λ)a,λc).
=(-λa,(1-λ)a,λc).
∵BE=![]() a,
a,
∴(-λa)2+[(1-λ)a]2+(λc)2=![]() . ①
. ①
∵BE⊥PC,∴λa2-(1-λ)a2+λc2=0.
∴c2=![]() =a2. ②
=a2. ②
由①②解得λ=![]() ,c=a,
,c=a,
∴E![]() ,P(0,0,a).
,P(0,0,a).
若存在满足条件的点F,可设AF=l(0≤l≤a),
则F(l,0,0),![]() .
.
设平面PAG的法向量为n=(s,t,p),
则 ∴n=(-2,1,0).
∴n=(-2,1,0).
∵EF∥平面PAG,∴![]() ·n=0.
·n=0.
∴-2l+![]() a-
a-![]() a=0,∴l=
a=0,∴l=![]() a.
a.
∴存在满足条件的点F,且AF=![]() a.
a.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,E,F,G分别是A1D1,D1D,D1C1的中点.

(1)求证:EG∥AC;
(2)求证:平面EFG∥平面AB1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|3x﹣ ![]() |.
|.
(1)求不等式f(x)<1的解集;
(2)若实数a,b,c满足a>0,b>0,c>0且a+b+c= ![]() .求证:
.求证: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,判断函数![]() 与函数
与函数![]() 的图象公共点个数,并说明理由;
的图象公共点个数,并说明理由;
(3)当![]() 时,函数
时,函数![]() 的图象始终在函数
的图象始终在函数![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A-BCDE中,底面BCDE是等腰梯形,BC∥ DE,∠ DCB=45°,O是BC中点,AO=![]() ,且BC=6,AD=AE=2CD=
,且BC=6,AD=AE=2CD=![]() .
.
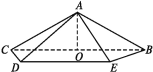
(1)证明:AO⊥平面BCD;
(2)求二面角A-CD-B的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1 , A2 , A3和3个欧洲国家B1 , B2 , B3中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2![]() ,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.
,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com