
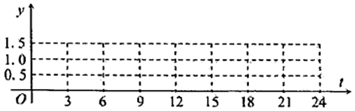
| t��ʱ�� | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y���ף� | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
���� ����ֱ�Ӹ��ݱ���������㣻
������ͼ��֪Ӧѡ��ĺ���ģ��Ϊ��y=Acos����t+�գ�+b������$\left\{\begin{array}{l}{A+b=1.5}\\{-A+b=0.5}\end{array}\right.$���A��b��ֵ��
������������æأ�������ͼ����һ����ߵ��һ����͵��������æ�ֵ����������ʽ����
�����ɣ�����0.5cos$\frac{��}{6}t$+1��1.25�������Dz���ʽ�ô𰸣�
��� �⣺�����ɱ������������ͼ��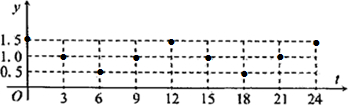 ��
��
������ͼ��֪��Ӧѡ��ĺ���ģ��Ϊ��y=Acos����t+�գ�+b��
������A��0���أ�0��
��A=$\frac{1.5-0.5}{2}=0.5$��b=$\frac{1.5+0.5}{2}=1$��$\frac{2��}{��}=12$����=$\frac{��}{6}$��
��y=0.5cos��$\frac{��}{6}t+$�գ�+1��
�ֵ�x=0ʱ��y=1.5��
��0.5cos��+1=1.5����cos��=1�����=2k��k��Z��
��y=0.5cos��$\frac{��}{6}t+$2k��+1=0.5cos$\frac{��}{6}t$+1����0��t��24����
������0.5cos$\frac{��}{6}t$+1��1.25����cos$\frac{��}{6}t$$��\frac{1}{2}$��
��$2k��-\frac{��}{3}��\frac{��}{6}t��2k��+\frac{��}{3}$����12k-2��t��12k+2��k��Z��
��8��t��20����10��t��14��
��һ���ڵ�8��00��20��00֮����4��Сʱ�ɹ����˰����߽��л��
���� ���⿼�麯��ģ�͵�ѡ��Ӧ�ã��������ѧ��ģ˼�뷽���������ȡͼ����������ѵ�������Dz���ʽ�Ľⷨ�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��t����x1 | B�� | f��t����x1 | C�� | f��t����x1 | D�� | f��t����x1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{4}{9}$ | C�� | $\frac{5}{9}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��+�ޣ� | B�� | ��-�ޣ�0�� | C�� | ��-�ޣ�e4�� | D�� | ��e4��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij��ѧ��ȤС��35��ѧ���ijɼ��ľ�Ҷͼ��ͼ��ʾ������ѧ���ijɼ��ɸߵ��ͱ�Ϊ1��35�ţ�����ϵͳ�����������г�ȡ7�ˣ������гɼ�������[70��85���ϵ�ѧ��������5��
ij��ѧ��ȤС��35��ѧ���ijɼ��ľ�Ҷͼ��ͼ��ʾ������ѧ���ijɼ��ɸߵ��ͱ�Ϊ1��35�ţ�����ϵͳ�����������г�ȡ7�ˣ������гɼ�������[70��85���ϵ�ѧ��������5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com