Question

【题目】如下图，在三棱锥 中， ， ， 为 的中点.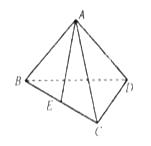

（1）求证： ；
（2）设平面 平面 ， ， ，求二面角 的正弦值.

Answer 1

【答案】
（1）证明：设 的中点为 ，连接 ，∵ ，∴ ，
又∵ 为 的中点，∴ ，∵ ，∴ ．
∵ ，∴ 平面 ，
又∵ 平面 ，
∴
（2）解：由（1）知： ， ，
∵平面 平面 ，
平面 平面 平面 ，
∴ 平面 ，∵ 平面 ，
∴ ，∴ 两两互相垂直．
∵ ，∴ ．
由 为 的中点， 得 ，
以 为坐标原点，建立如图所示的空间直角坐标系 ，则 ，
∴ ．
设平面 的一个法向量为 ，则 ．
∴ ，取 ，解得 ，
∴ 是平面 的一个法向量．
同理可求平面 的一个法向量 ．
设二面角 的大小为 ，则 ，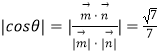
∵ ，∴ ，
二面角 的正弦值为 ．

【解析】（1）通过直线与平面垂直证明直线与直线垂直；
（2）建立空间直角坐标系，求出平面的法向量，利用法向量的夹角求二面角.
【考点精析】通过灵活运用直线与平面垂直的判定和直线与平面垂直的性质，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；垂直于同一个平面的两条直线平行即可以解答此题．