
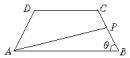
如图等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.
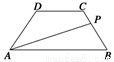
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.
(1)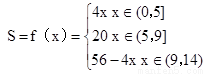 (2)20
(2)20
【解析】本小题主要函数模型的选择与应用.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.
(1)先作出所需辅助线:过C点作CE⊥AB于E,再分类讨论求出:在当x∈(0,5]时,当x∈(5,9]时,当x∈(9,14]时,函数S=f(x)表达式即可;
(2)分类讨论:当x∈(0,5]时,当x∈(5,9]时,当x∈(9,14]时,分别求出各个区间上的最大值,最后综合即得,△ABP的面积S最大值即可.
解(1)过C点作CE⊥AB于E,
在△BEC中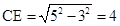 ,∴
,∴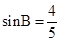
由题意,当 时,过P点作PF⊥AB于F,
时,过P点作PF⊥AB于F,
∴PF=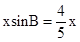 ,∴当
,∴当 时,
时,
当 时,
时,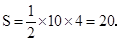
当 时,
时,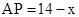

∴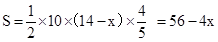 .综上可知,
.综上可知,
函数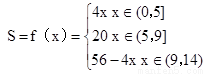
(2)由(1)知,当 时,f(x)=4x为增函数,
时,f(x)=4x为增函数,
所以,当x=5时,取得最大值20.
当x∈(5,9]时,f(x)=20,最大值为20.当x∈(9,14]时,f(x)=56-4x为减函数,无最大值.
综上可知:当P点在CD上时,△ABP的面积S最大为20.


科目:高中数学 来源:数学教研室 题型:022
查看答案和解析>>
科目:高中数学 来源:山东省济宁市重点中学2012届高三上学期期中考试数学理科试题 题型:044
建造一条防洪堤,其断面为如图等腰梯形ABCD,腰与底边所成角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为6![]() 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小.
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小.

(1)求外周长的最小值,此时防洪堤高h为多少?
(2)如防洪堤的高限制在[3,3![]() ]范围内,外周长最小为多少米?
]范围内,外周长最小为多少米?
查看答案和解析>>
科目:高中数学 来源:山西省忻州一中2012届高三上学期期中考试数学理科试题 题型:044
建造一条防洪堤,其断面为如图等腰梯形ABCD,腰与底边所成角为60°
,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为6![]() 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长梯形的上底线段与两腰长的和)要最小.
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长梯形的上底线段与两腰长的和)要最小.

(1)求外周长的最小值,此时防洪堤高h为多少?
(2)如防洪堤的高限制在[3,3![]() ]范围内,外周长最小为多少米?
]范围内,外周长最小为多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
建造一条防洪堤,其断面为如图等腰梯形ABCD,腰与底边所成角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为6![]() 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小.
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小.
(1) 求外周长的最小值,此时防洪堤高h为多少?
(2) 如防洪堤的高限制在[3,3![]() ]范围内,外周长最小为多少米?
]范围内,外周长最小为多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com